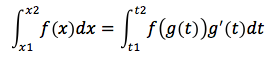Nel seguito considereremo insiemi i cui elementi sono numeri reali. Insiemi di particolare importanza sono gli intervalli che si definiscono nel modo seguente: se a e b sono due numeri reali con a < b, l'insieme di tutti i numeri reali compresi fra a e b si chiama intervallo. Il numero a si chiama estremo inferiore, il numero b si chiamano estremo superiore dell'intervallo. Tenendo presente che esiste una corrispondenza biettiva tra numeri reali e punti della retta queste due nozioni si potranno tranquillamente confondere e quindi un intervallo (insieme di numeri reali) è riconducibile ad un segmento (insieme di punti) sulla retta R. Questa corrispondenza biunivoca permette di dare un significato geometrico a tutte le nozioni introdotte per gli insiemi di numeri reali. L'ampiezza dell'intervallo si determina facendo la differenza b-a che è in pratica la misura del segmento. Il numero (a+b)/2 è il centro dell'intervallo, il numero (b-a)/2 è il raggio dell'intervallo. Se gli estremi dell'intervallo appartengono all'intervallo stesso allora l'intervallo si dice chiuso e si indica con il simbolo [a,b], se a, b non appartengono all'intervallo allora l'intervallo stesso si dice aperto e si indica con ]a,b[.
Un intervallo può anche essre aperto a sinistra e si indicherà ]a,b] oppure aperto a destra [a,b[. Gli intervalli possono essere illimitati e si definiscono nel modo seguente: sia a un qualunque punto della retta, si chiama intervallo illimitato l'insieme di tutti i numeri reali non minori di a e si indica [a,+∞[ (a si chiamerà estremo inferiore). Analogamente, l'insieme di tutti i numeri reali non maggiori di a si indicherà con ]-∞,a], (in questo caso a si chiamerà estremo superiore). Gli intervalli illimitati, così definiti, corrispondono alle semirette in R.
Definizione: si dice intorno di un punto x, ogni intervallo aperto che contiene x.
Definizione: si dice intorno centrato di un punto x, ogni intervallo aperto che ha il punto x come centro.
Definizione: si dice intorno destro di un punto x, ogni intervallo aperto a destra che abbia x come estremo inferiore.
Ad esempio l'intervallo [4,9[ è un intorno destro del punto (o del numero) 4. Analogamente si definisce l'intorno sinistro di un punto x.
Definizione: si dice intorno di infinito ogni insieme di punti che soddisfano ad una condizione del tipo ׀x׀>k, dove k è un numero reale.
Definizione: si dice intorno di +infinito ogni insieme di punti che soddisfano ad una condizione del tipo x>k dove k è un numero reale.
Analogamente si definisce l'intorno di -infinito.
Definizione: sia V un insieme di punti sulla retta, si dice che P è punto di accumulazione rispetto all'insieme V se, in ogni intorno di P cadono infiniti punti di V.
Esempio 1: consideriamo come insieme V l'aperto ]3,7[ ogni punto dell'intervallo stesso compresi gli estremi 3 e 7 sono punti di accumulazione per l'insieme V .
Esempio 2: consideriamo l'insieme V:{x ∈R: x=1/n, n∈N(insieme dei numeri naturali}. Si noti che V non è un intervallo ma un insieme di punti isolati. (un punto di un certo insieme V si dice isolato se esiste un intorno del punto stesso in cui non cade alcun punto dell'insieme V). Verifichiamo che lo zero è punto di accumulazione per l'insieme V. A questo scopo si osservi che ∀ ε > 0, nell'intervallo [0,ε[, cadono infiniti punti di V ovvero tutti gli n che soddisfano alla condizione n>1/ ε e quindi in ogni intorno destro dello zero cadono infiniti punti di V.
I termini "continuo" e "continuità" sono usati nel linguaggio comune per indicare una linea che viene disegnata con un pennino su un foglio di carta, senza sollevare il pennino dal foglio. È quello che avviene spesso in molti fenomeni naturali come, per esempio, la crescita di un essere vivente. La crescita avviene in modo continuo e l'essere vivente raggiunge una certa statura, passando per tutte le stature intermedie, senza salti. Un fenomeno fisico che invece viene rappresentato con una linea non continua è quello del volume dell'acqua in funzione della temperatura. Il grafico ha un andamento continuo nel tratto in cui la temperatura è negativa, in cui l'acqua si presenta sotto forma di ghiaccio ed anche nel tratto in cui la temperatura è positiva in cui l'acqua è allo stato liquido. Nel punto 0° c'è un salto, infatti è il punto di passaggio dallo stato solido allo stato liquido. Com'è noto, il ghiaccio, trasformandosi in acqua, occupa minor volume. La funzione non è continua, per disegnarla, infatti, bisogna sollevare il pennino dal foglio.
Una funzione f definita in A (A ⊂ R) si dice continua (localmente) in un punto x0 (x0 ∈ A) se: per ogni intorno U di f(x0), esiste un intorno V di x0 tale che, per ogni punto x di V (appartenente ad A) ne consegue che f(x) appartenente ad U
In simboli: ∀ U(f(x0)), ∃ V(x0):∀ x ∈ V(x0), (x∈A) ⇒ f(x) ∈U(f(x0))
Una funzione si dice (globalmente) continua in un insieme A se la definizione di continuità locale e' verificata per ogni elemento dell'insieme A.
Dalla definizione ne consegue, in particolare, che se x0 è punto isolato di A, ogni f definita in A è da considerarsi continua in x0.
Una funzione continua definita su un intervallo "ha l'aspetto" di una linea. La funzione f(x)=x, in cui il dominio sia A = {0,1,2,3,4,5,6}, è una funzione formata da sette punti, si tratta comunque di una funzione continua anche se non ha l'aspetto di una linea e questo appunto perchè il dominio è costituito da un insieme di punti isolati e quindi la definizione di continuità locale è rispettata.
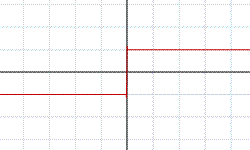
In figura compare la funzione f(x)=x/lxl, anche se fa un "salto" nell'origine del sistema di riferimento, è continua è ciò perché è definita in R-{0}.
Si noti quindi che l'ipotesi che la f sia definita in un intervallo è essenziale perchè la funzione continua abbia l'aspetto di una linea continua.
Definizione: sia f definita su A, e sia x0 punto di accumulazione per A; si dice che la f è continua a sinistra di x0 se è continua ogni sua restrizione all'insieme A = {x: x ∈ A, x ≤ x0}.
Analogamente la definizione di continuità a destra. È chiaro che se una funzione è continua in x0, è continua sia a sinistra che a destra di x0.
Definizione: si chiamano massimo M e minimo m, di una funzione su un intervallo V, rispettivamente il più grande e il più piccolo dei valori assunti dalla funzione in V.
Una funzione continua definita in un intervallo chiuso e limitato [a,b] è dotata di massimo e minimo. Il teorema dice che, se una funzione è continua in un chiuso [a,b], allora il suo insieme immagine è limitato ovvero esistono due punti x1, x2 ⋲ [a,b]: f(x1)= M, f(x2) = m
Una funzione continua definita in un intervallo V, se assume due valori distinti y1, y2, assume necessariamente ogni valore y intermedio.
Una funzione continua definita in un intervallo V, se assume in due punti x1, x2 ∈ V, valori di segno opposto, allora ∃ almeno un punto x: x1<x<x2: f(x)=0.
Sia fr la restrizione della f all'insieme A - {x0}. Della continuità della f in x0 rimane qualcosa alla fr? I termini nei quali la continuità si esprime non hanno più significato per la fr, la quale non ha alcun valore in x0, però, il fatto che i valori della f per x prossimo ad x0 "sono prossimi" al numero f(x0), che indichiamo con l, può esprimersi anche per la fr: i suoi valori per x prossimo ad x0 (e diverso da x0, e naturalmente x∈ A) "sono prossimi" al numero l.
Spesso accade il contrario: che una funzione f non sia definita in un punto x0 e che la si possa estendere attribuendole in x0 un valore in modo che essa (o meglio la sua estensione) risulti continua in x0. Tale valore evidentemente, dovrà venire desunto dal comportamento della funzione in prossimità di x0. Quindi la funzione f ha come limite l, per x che tende ad x0, e si scrive: limx→x0 f(x) = l , se ponendo f(x0) = l, la funzione risulta continua in x0. Come esempio consideriamo la funzione f(x) = (x-1)(x+3)/(x-1) la quale è definita in R-{1} (Si tratta della retta y=x+3 con un "buco" nel punto x0=1). Ponendo f(1)=4 la funzione prolungata su A U {1} risulta continua. In tal caso il punto 1 è di accumulazione per il dominio della f, ovviamente si ha che il limite esiste ed è: limx→1=4.
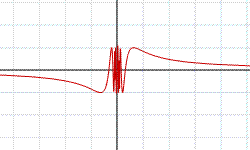
In figura è rappresentata la funzione f(x)=sin(1/x) definita per ogni x eccetto che per x=0.
Non è possibile assegnare un valore alla f nel punto 0 in modo da renderla continua perché in ogni intorno di 0 la f assume tutti i valori dell'intervallo {y: -1≤y≤1 }, mentre per raggiungere il nostro scopo, al restringersi della variabilità di x intorno a 0 i valori della f dovrebbero restringersi intorno ad un numero l.
Attraverso questo esempio si può notare che non sempre una funzione si comporta, in prossimità di un punto x0 , così come la restrizione fr di una funzione che in x0 sia continua. In questo caso il limite per x tendente a 0 non esiste.
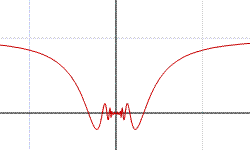
Per quanto riguarda invece la funzione
f(x) = xsin(1/x) in figura
che è definita in A=R-{0} , con 0 punto
di accumulazione per A, si ha:
limx→0 xsin(1/x) = 0.
Ponendo f(0)=0 la funzione prolungata su tutto R risulta continua.
Si dice che una funzione f, definita in A, ha come limite il numero l al tendere di x verso x0 (punto di accumulazione di A) se: per ogni intorno U di l, esiste un intorno V di x0, tale che, per ogni x di A appartenente a V-{x0} ne consegue che f(x) appartiene a U.
In simboli:
1. ∀ U(l), ∃ V(x0): ∀ x ∈ V-x0, (x∈A) ⇒ f(x) ∈ U.
Oppure, che è lo stesso:
2. ∀ U(l), ∃V(x0): ∀ x ∈ V-{x0} (x∈A) ⇒ f(x) ∈ U, con U e V intorni centrati di raggio δ e ε.
Oppure, che è lo stesso:
3. ∀ ε > 0, ∃δ >0: ∀ x: ׀x-x0 ׀ < δ (x∈A) ⇒ ׀f(x) - l׀ < ε.
Oppure, che è lo stesso:
4. ∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x) - l׀ < ε
Teniamo presente che la definizione può essere suddivisa in quattro parti. Di definizioni ne sono scritte quattro, ma tutte tra di loro equivalenti. La 1. fa riferimento agli intorni, la 2. agli intorni centrati, la 3. ai raggi degli intorni centrati, la 4. ha riferimenti misti, ovvero la prima e la quarta parte riportano i raggi, la seconda e la terza parte gli intorni. In ogni caso, la prima e la quarta parte interessano l'asse delle y, la seconda e la terza l'asse x. La 1. è sicuramente più "intuitiva", la 2. costituisce una sorta di passaggio di consegne tra gli intorni e i raggi stessi, la 3. e la 4. sono più utilizzabili nei calcoli, per verificare, per esempio, un limite.
| Prima parte | Seconda parte | Terza parte | Quarta parte |
| ∀ U(l), | ∃ V(x0): | ∀ x ∈ V-x0, (x∈A), | ⇒ f(x) ∈ U |
| ∀ U( di centro l), | ∃ V( di centro x0): | ∀ x ∈ V-x0, (x∈A), | ⇒ f(x) ∈ U |
| ∀ ε > 0, | ∃ δ > 0: | ∀ x: ׀x-x0׀ < δ (x∈A), | ⇒ ׀f(x) - l׀ < ε |
| ∀ ε > 0, | ∃ V(x0): | ∀ x ∈ V-x0, (x∈A), | ⇒ ׀f(x) - l׀ < ε |
L'essere f continua in x0 (punto di accumulazione per A) equivale ad essere: limx→x0 f(x) = f(x0) ed infatti enunciare la definizione di continuità equivale ad enunciare la definizione di limite con f(x0) al posto di l.
Limite infinito, limite per x→∞ .
Non possiamo pensare di trattare +∞, -∞ come due qualsiasi altri numeri pensando che +∞ segua tutti i punti di R e -∞ li preceda tutti, anche se ciò potrebbe dare dei vantaggi dal punto di vista della struttura d'ordine. Dal punto di vista algebrico però, ogni tentativo di estendere ai nuovi enti l'addizione e la moltiplicazione porterebbe a far cadere qualcuna delle proprietà formali, si pensi di dar significato per esempio al seguente prodotto: 0(+∞), oppure alla seguente somma:(+∞) + (-∞). Allora rinunciamo ad aggiungere +∞,-∞ all'insieme dei numeri reali, ma continuiamo a chiamare intorno di +∞ ogni intervallo del tipo {x: x>a}. Per i numeri l'assenza di un segno preposto sottointende che sono positivi, per il caso dell'infinito la convenzione di scrittura è diversa per cui intorno di ∞ è ogni insieme del tipo {x: lxl>a}; ∞ è di accumulazione per A se ogni intorno di ∞ contiene punti di A. A questo punto, risulterà naturale estendere la definizione di limite anche quando in luogo di x0 oppure di l vi sia uno dei simboli +∞, -∞, ∞.
Per esempio limx→x0 f(x) = -∞ (presupposto che x0 sia di accumulazione per A) significa che: per ogni intorno U di -∞ , esiste un intorno V di x0, tale che, per ogni x appartenente a V-{x0} ne consegue che f(x) appartiene a U.
In simboli:
∀U(-∞), ∃ V(x0): x ∈ V-{x0}, (x∈A) f(x) ∈ U. O che è lo stesso
∀U(-∞), ∃V(x0): ∀ x ∈ V-{x0}, (x∈A) ⇒ f(x) ∈ U, con V intorno centrato di raggio δ. O che è lo stesso:
∀ k, ∃δ >0: x: ׀x-x0׀ < δ, (x∈A) ⇒ f(x)<k. O che è lo stesso:
∀ k, ∃ V(x0): x ∈ V-x0, (x∈A) ⇒ f(x) < k.
Vediamo un altro esempio: limx→-∞ f(x) = +∞ significa che:
per ogni intorno U di +∞ , esiste un intorno V di -∞, tale che, per ogni x appartenente a V ne consegue che f(x) appartiene a U
in simboli:
∀U(+∞ ), ∃ V(-∞): x ∈ V, (x∈A) ⇒ f(x) ∈ U.
O che è lo stesso: ∀ k, ∃ h: x: x < h, (x∈A) ⇒ f(x) > k.
O che è lo stesso:
∀ k, ∃ V(x0): x ∈ V, (x∈A) ⇒ f(x) > k
Nel caso in cui si parli di intorni di +∞ oppure -∞ il concetto di intorno centrato viene a perdersi.
Nella funzione sinx/x valgono i seguenti limiti: limx→+∞sinx/x=0, limx→-∞sinx/x=0, ciò si può esprimere scrivendo limx →∞ sinx/x =0, ovvero questo limite congloba i due precedenti.
Si noti quindi che
l'essere: limx→+∞ f(x)= l,
limx→-∞ f(x)= l
( l finito o no) equivale all'essere: limx→∞
f(x)= l, e
questo significa che:
∀ ε >
0, ∃ k: ∀x: lxl>k, ⇒ lf(x)-ll<ε
Allo stesso modo come si è provato che, per x→x0, f(x) non può avere due limiti finiti distinti, è facile provare che, per x→x0 (oppure +∞, -∞ in luogo di x0), f(x) non può avere un limite finito e un limite infinito, né può tendere simultaneamente a +∞ oppure -∞.
Dall'essere limx→x0 f(x) = ∞, non segue che il limite stesso possa precisarsi con +∞ oppure -∞.
Nella figura è rappresentata la funzione x/sinx che è la reciproca della precedente.
È: limx→+∞ x/sinx= ∞, questo perché lx/sinx l≥lxl, ma la funzione, non tende a +∞ 0-∞.
L'affermazione limx→+∞f(x)=∞ significa che: per ogni numero reale h, esiste un numero reale k tale che per x>k si abbia ׀f(x)׀>h
in simboli: ∀ h ∈ R, ∃ k ∈ R: se x > k → ׀f(x)׀>h
A volte interessa il comportamento di
una funzione a sinistra o a destra di x0, ossia il
comportamento per x tendente a x0 delle restrizioni
della f agli insiemi {x: x<x0} e {x: x>x0}
sempre che x appartenga ad A e x0 sia di
accumulazione per i due insiemi. Se la restrizione a sinistra ammette
limite l per
x→ x0 esso si dice limite sinistro della f
per x→ x0 e si esprime
scrivendo: limx→xo- f(x)= l. Analogamente
si esprime il limite destro. L'esistenza del limite per x→x0 della
f(x) se x0 è di accumulazione per entrambi gli
insiemi considerati, equivale al fatto che il limite destro ed il
limite sinistro sono entrambi corrispondenti ad l.
Per il calcolo del limite ci saranno utili seguenti teoremi:
Teorema 1 Il limite di una somma di funzioni e' uguale alla somma dei limiti.
Teorema 2 Il limite di un prodotto di funzioni e' uguale al prodotto dei limiti.
Teorema 3 Il limite di un rapporto di funzioni e' uguale al rapporto dei dei limiti.
Dimostriamo il teorema 1
Ipotesi: Siano f, g funzioni definite su un certo dominio A, escluso al più un punto x0 che sia punto di accumulazione per A. Valgano inoltre i seguenti limiti: limx→x0 f(x)=l limx→x0 g(x)=m. Si intende che i limiti indicati con le lettere l, m, assumono valori reali finiti.
Tesi: limx→x0 f(x)+g(x)=l+m
Dimostrazione: Per la definizione di limite avremo:
∀ ε' > 0, ∃ V'(x0): ∀ x ∈ V'-x0, (x∈A), ⇒ ׀f(x) - l׀ < ε'
∀ ε'' > 0, ∃ V''(x0): ∀ x ∈ V''-x0, (x∈A), ⇒ ׀g(x) - m׀ < ε''
Bisogna dimostrare che vale la seguente definizione:
∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x)+g(x) - l - m׀ < ε
tenendo presente che per la proprietà dei valori assoluti si ha che: ׀f(x)+g(x) - l - m׀ > ׀f(x) - l׀ + ׀g(x) - m׀ e che quest'ultima espressione risulta < ε'+ε'' basta prendere ε ≥ ε'+ε'' per la proprietà transitiva della disuguaglianza la definizione del limite della funzione somma risulta essere soddisfatta.
La dimostrazione degli altri due teoremi risulta essere pressochè analoga e sfrutta ancora la definizione di limite. Da questi teoremi, si possono trarre delle regole che facilitano il calcolo del limite.
La prima regola è sostituire il valore a cui tende la variabile x nell'espressione analitica della funzione stessa. Ma cosa succede quando i due limiti non sono finiti? Per esempio può, presentarsi il caso in cui il limite della funzione f sia finito e quello della funzione g +∞, in tal caso il limite della funzione somma è +∞. Nelle tabelle sono presentati tutti i casi che si verificano.
| lim f | lim g | lim f+g |
| l | m | l+m |
| l | +∞ | +∞ |
| l | -∞ | -∞ |
| +∞ | +∞ | +∞ |
| -∞ | -∞ | -∞ |
| +∞ | -∞ | ind |
| lim f | lim g | lim f*g |
| l | m | l*m |
| +∞ | +∞ | +∞ |
| +∞ | -∞ | -∞ |
| -∞ | -∞ | +∞ |
| l | ∞ | ∞ |
| ∞ | 0 | ind |
| lim f | lim g | lim f/g |
| l | m | l/m |
| l | ∞ | 0 |
| ∞ | l | ∞ |
| l | 0 | ∞ |
| ∞ | ∞ | ind |
| 0 | 0 | ind |
Si può notare che la funzione somma ha il caso indeterminato +∞-∞, la funzione prodotto il caso 0*∞, la funzione rapporto ha due casi indeterminati 0/0 ed ∞/∞. In tali casi non ci sono teoremi che permettono di stabilire il limite a priori, ma, caso per caso, sono necessarie ulteriori analisi per eseguire il calcolo. Nella sezione esercitazioni sono presenti alcuni esercizi guida che presentano le tecniche più comuni per risolvere i casi indeterminati.
Nelle seguenti righe, facendo sempre riferimento alla definizione di limite, si dimostano tre importanti teoremi.
Ipotesi: Sia f una funzione definita su un certo dominio A, escluso al più un punto x0 che sia punto di accumulazione per A. Valga inoltre il seguente limite: limx→x0 f(x)=l
Tesi: il limite è unico.
Nota: La dimostrazione di questo teorema è particolare in quanto è una dimostrazione per assurdo. Tale dimostrazione sfrutta l'equivalenza delle due tipologie dimostrative:
1. diretta: ipotesi → tesi
2. per assurdo: non tesi → non ipotesi
La dimostrazione in generale più usata è quella diretta, però, questo teorema conviene dimostrarlo partendo dalla non tesi, arrivando, attraverso la dimostrazione, alla non ipotesi.
Dimostrazione:
Partire dalla non tesi significa quindi ammettere l'esistenza di due limiti diversi l, l' per x → x0 ovvero:
limx→x0 f(x)=l
limx→x0 f(x)=l'
Per come sono stati scritti i due limiti supponiamo, per ora, che sia il valore x0 che il valore l siano finiti. Per la definizione di limite avremo contemporaneamente:
∀ U(l), ∃ V(x0): ∀ x ∈ V-x0, (x∈A) ⇒ f(x) ∈ U
∀ U'(l), ∃ V'(x0): ∀ x ∈ V '-x0, (x∈A) ⇒ f(x) ∈ U'
U ed U' possiamo pensarli disgiunti ovvero U∩U'=∅ e in V ∩ V', che è ancora un intorno di x0 le definizioni scritte devono valere contemporaneamente. Per tanto succede che prendendo un valore x appartenente a V ∩ V' la relativa f(x) deve cadere contemporaneamente sia in U che in U'. Ad un valore del dominio corrisponderebbero due nell'insieme immagine quindi la f non sarebbe più una funzione e ciò va contro l'ipotesi. A questo punto è stato dimostrato il teorema non tesi → non ipotesi che è equivalente al teorema ipotesi → tesi. Il limite è quindi unico. Analogamente si può dimostrare il teorema nel caso in cui il valore del limite ed il valore a cui tende x siano uno finito ed uno infinito oppure entrambi i valori siano infiniti.
Ipotesi:
Siano f, g, h, tre funzioni definite sullo stesso dominio A, escluso al più un punto x0 che sia punto di accumulazione per A.
Per ogni x appartenente ad A si abbia f(x) ≤ g(x) ≤ h(x).
Valgano inoltre i seguenti limiti: limx→x0 f(x)=l, limx→x0 h(x)=l
Tesi: limx→x0 g(x)=l
Dimostrazione:
Per la definizione di limite applicata alla f si ha che: ∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x)- l׀ <ε
Per la definizione di limite applicata alla h si ha che: ∀ ε > 0, ∃ V'(x0): ∀ x ∈ V'-x0, (x∈A), ⇒ ׀h(x)- l׀ <ε
In V ∩ V', che è ancora intorno di x0, valgono contemporaneamente sia ׀f(x)- l׀ <ε che ׀h(x)- l׀ <ε
queste ultime due relazioni, che sono disequazioni con valori assoluti, sono equivalenti a:
l-ε <f(x) <l+ε e rispettivamente a:
l-ε <h(x) < l+ε
Tenendo quindi conto anche delle ipotesi, in V ∩ V' si avrà l-ε < f(x) ≤ g(x) ≤ h(x) < l+ε
quindi l-ε < g(x) < l+ε o che è lo stesso: ׀g(x)- l׀ <ε
Quindi si è dimostrato che ∀ ε > 0, ∃ V ∩ V'(x0): ∀ x ∈ V ∩ V'-x0,(x∈A), ⇒ ׀g(x)- l׀ <ε
Ciò vuol dire, in base alla definizione di limite che:
limx→x0 g(x)=l.
Il nome del teorema, ricorda quindi che la funzione g deve confrontarsi con le f e h ovvero, le funzioni f e h rappresentano i due carabinieri che costringono la g a fare lo stesso loro percorso che, presumibilmente, finirà in galera.
Ipotesi:
Sia f(x) una funzione definita in un dominio A escluso al più un punto x0 che sia punto di accumulazione per A.
Valga il seguente limite: limx→x0 f(x)=l
Tesi:
Esiste un intorno di x0, escluso x0 stesso, in cui la funzione assume lo stesso segno di l.
Dimostrazione:
Supponiamo che l sia positivo, per definizione si ha che: ∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x)- l׀ <ε, scegliamo ε=l/2, avremo quindi che ׀f(x)- l׀ <l/2, sviluppando il valore assoluto si trova che: l-l/2<f(x)<l+l/2 ovvero l/2<f(x)<3l/2. Si è così dimostrato che esiste un intorno di x0, in cui la funzione assume valori positivi. Analogamente si può dimostare che il teorema vale anche nel caso in cui il limite assume valore negativo.
Dimostriamo due teoremi sui limiti, considerando, per semplicità, solamente il caso in cui, sia il valore a cui tende la variabile, sia i limiti a cui tendono le funzioni, siano finiti.
Sia f una funzione definita su un certo dominio A, escluso al più un punto x0 che sia punto di accumulazione per A.
Valga inoltre il seguente limite: limx→x0 f(x)=l
Tesi:
il limite è unico.
Nota:
La dimostrazione di questo teorema è particolare in quanto è una dimostrazione per assurdo. Tale dimostrazione sfrutta l'equivalenza delle due tipologie dimostrative:
1. diretta: ipotesi → tesi
2. per assurdo: non tesi → non ipotesi
La dimostrazione in generale più usata è quella diretta, però, questo teorema conviene dimostrarlo partendo dalla non tesi, arrivando, attraverso la dimostrazione, alla non ipotesi.
Dimostrazione:
Partire dalla non tesi significa quindi ammettere l'esistenza di due limiti diversi l, l' per x → x0 ovvero:
limx→x0 f(x)=l
limx→x0 f(x)=l'
Per come sono stati scritti i due limiti supponiamo, per ora, che sia il valore x0 che il valore l siano finiti. Per la definizione di limite avremo contemporaneamente:
∀ U(l), ∃ V(x0): ∀ x ∈ V-x0, (x∈A) ⇒ f(x) ∈ U
∀ U'(l), ∃ V'(x0): ∀ x ∈ V'-x0, (x∈A) ⇒ f(x) ∈ U'
U ed U' possiamo pensarli disgiunti ovvero U∩U'=∅ e in V ∩ V', che è ancora un intorno di x0 le definizioni scritte devono valere contemporaneamente. Per tanto succede che prendendo un valore x appartenente a V ∩ V' la relativa f(x) deve cadere contemporaneamente sia in U che in U'. Ad un valore del dominio corrisponderebbero due nell'insieme immagine quindi la f non sarebbe più una funzione e ciò va contro l'ipotesi. A questo punto è stato dimostrato il teorema non tesi → non ipotesi che è equivalente al teorema ipotesi → tesi. Il limite è quindi unico. Analogamente si può dimostrare il teorema nel caso in cui il valore del limite ed il valore a cui tende x siano uno finito ed uno infinito oppure entrambi i valori siano infiniti.
Ipotesi:
Siano f, g, h, tre funzioni definite sullo stesso dominio A, escluso al più un punto x0 che sia punto di accumulazione per A.
Per ogni x appartenente ad A si abbia f(x) ≤ g(x) ≤ h(x).
Valgano inoltre i seguenti limiti: limx→x0 f(x)=l, limx→x0 h(x)=l
Tesi: limx→x0 g(x)=l
Dimostrazione:
Per la definizione di limite applicata alla f si ha che: ∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x)- l׀ <ε
Per la definizione di limite applicata alla h si ha che: ∀ ε > 0, ∃ V'(x0): ∀ x ∈ V'-x0, (x∈A), ⇒ ׀h(x)- l׀ <ε
In V ∩ V', che è ancora intorno di x0, valgono contemporaneamente sia ׀f(x)- l׀ <ε che ׀h(x) l׀ <ε
queste ultime due relazioni, che sono disequazioni con valori assoluti, sono equivalenti a:
l-ε <f(x) <l+ε e rispettivamente a:
l-ε <h(x) < l+ε
Tenendo quindi conto anche delle ipotesi, in V ∩ V' si avrà l-ε < f(x) ≤ g(x) ≤ h(x) < l+ε
quindi l-ε < g(x) < l+ε o che è lo stesso: ׀g(x)- l׀ <ε
Quindi si è dimostrato che ∀ ε > 0, ∃ V ∩ V'(x0): ∀ x ∈ V ∩ V'-x0,(x∈A), ⇒ ׀g(x)- l׀ <ε
Ciò vuol dire, in base alla definizione di limite che:
limx→x0 g(x)=l.
Il nome del teorema, ricorda quindi che la funzione g deve confrontarsi con le f e h ovvero, le funzioni f e h rappresentano i due carabinieri che costringono la g a fare lo stesso loro percorso che, presumibilmente, finirà in galera.
Il limite si presenta nella forma forma indeterminata del tipo 0/0. Bisogna valutare il comportamento della funzione sinx/x in un intorno dello zero e questo ci permette di considerare l'angolo x < π/2.
Pensando alla misura di senx e tanx possiamo scrivere che:
1. sinx<x<tanx
dove x rappresenta la lunghezza dell'arco sotteso dall'angolo x. La misura in radianti dell'angolo al centro che insiste sull'arco è x così come è x la misura dell'arco nell'unità di misura della lunghezza.
A questo punto consideriamo due casi facendo vedere che:
caso a. Limx→0+ sinx/x=1
caso b. Limx→0- sinx/x=1.
Caso a.
essendo sinx >0, dividendo ciascun termine per sinx non si altera il verso della 1. ottenendo:
1<x/sinx<1/cosx
quindi si passa ai reciproci invertendo il verso:
cosx<sinx/x<1
ed essendo Limx→0+ cosx=1 Limx→0+ 1=1 si può applicare il teorema del confronto poichè, come si nota anche in figura, la funzione sinx/x è compresa tra la funzione y=cosx e la funzione costante y=1. Si ottiene: Limx→0+ sinx/x=1
Caso b
essendo sinx <0, dividendo ciascun termine per sinx si inverte il verso della disuguaglianza e si ottiene:
1>x/sinx>1/cosx
osservando che a sinistra dello zero sinx<0, x<0 e cosx>0 passando ai reciproci si ottiene: 1>sinx/x>cosx
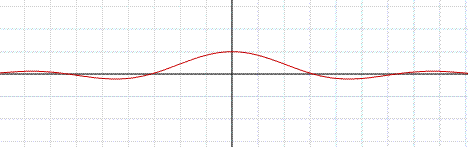
ed essendo Limx→0- cosx=1 si può applicare il teorema del confronto poichè, come nel primo caso, anche in un intorno dello zero, la funzione sinx/x è compresa tra la funzione y=cosx e la funzione costante y=1. Quindi, siccome: Limx→0+ sinx/x=1 poiché Limx→0- sinx/x=1 allora Limx→0 sinx/x=1 C.V.D.
Se si misurano gli angoli in gradi la disuguaglianza sinx<x<tanx deve essere sostituita dalla sinx<xπ/180<tanx come si ricava tenendo conto del legame tra la misura in gradi e in radianti di uno stesso angolo. Da qui segue che: Limx→0 sinx/x=π/180
Supponiamo che l’unità di misura degli angoli sia il radiante. Se sulla circonferenza goniometrica, che ha raggio uguale ad uno, prendiamo un arco di lunghezza pari a 1 allora, l’angolo che insiste su questo arco misura 1 radiante. Per definizione, infatti, il radiante è l’angolo al centro della circonferenza che sottende un arco di lunghezza pari al raggio. Più in generale, se sulla circonferenza goniometrica prendiamo un arco di lunghezza x allora l’angolo che insiste su questo arco avrà un’ampiezza di x radianti. Se il raggio della circonferenza goniometrica è uguale a 1 (per esempio 1cm) una sinusoide completa corrisponde a 2π (~6,28cm) sull'asse x.
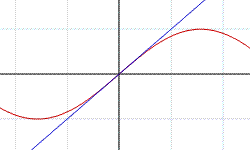
Dire che il limite per x tendente a zero del rapporto sinx/x vale uno, dal punto di vista grafico significa che la funzione y=x risulta essere tangente alla funzione sinx nell’origine, come si può notare in figura.
Diverse considerazioni vanno fatte nel caso in cui l’unità di misura sia il grado. In questo caso, considerato sempre che il raggio della circonferenza goniometrica è uguale a 1 (per esempio 1cm), ad un angolo giro corrisponde 360 (3,60m) sull'asse x, in altre parole, usando un linguaggio descrittivo, potremo dire che, il grafico della funzione seno, formerà una sinusoide piuttosto allungata. Si tenga presente che 1 grado corrisponde a π/180 (~0,01745) radianti. In questo caso la retta tangente alla funzione sinx sarà una retta passante comunque per l'origine, ma con un coefficiente angolare molto inferiore ad uno, ovvero la retta y= (π/180)x. Il limite per x tendente a zero del rapporto sinx/x è infatti π/180. In tutte le osservazioni di carattere grafico fatte, si è che usata, per il sistema di riferimento, la scala 1:1. Bisogna fare attenzione a non confondere il limite notevole appena dimostrato con il seguente: Limx→∞ sinx/x. In questo caso x non tende a zero bensì a infinito e la forma non è indeterminata essendo espressa da un rapporto tra una funzione limitata e una funzione che tende ad infinito. Si noti quindi che questo limite è uguale a zero. Si veda il grafico della funzione sinx/x in figura.

Si dimostra, ma omettiamo la dimostrazione, che questo limite esiste ed è un valore compreso tra 2 e 3, si indica con il simbolo ê si chiama il numero di Nepero ed è un numero irrazionale che, scritto in notazione decimale, approssimato per difetto alla dodicesima cifra dopo la virgola è: 2,718281828459. In figura il grafico della funzione (1+1/x)x che, come si nota, ha per asintoto orizzontale la retta y=ê.
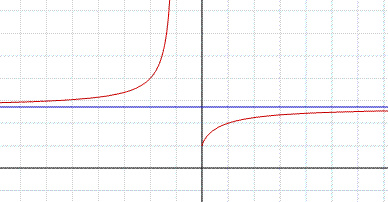
Il numero di Nepero entra in molti fenomeni naturali (per esempio la catenaria) e si assume come base nei logaritmi poiché le formule in cui intervengono i logaritmi in questa base, si presentano sotto un aspetto semplice.
| Ai | modesti | e | vanitosi | ai | violenti | e | timorosi | do | cantando | gaio | ritmo | logaritmo |
| La | sangria | è | squisita | da | ebbrezza | e | allegria | la | quantità | però | resti | contenuta |
| Lo | zampone | è | modenese | il | gianduia | è | torinese | le | tortelle | sono | tutte | bolognesi |
| La | bambina | è | affamata | la | minestra | è | squisita | la | scodella | vien | tosto | terminata |
| 2 | 7 | 1 | 8 | 2 | 8 | 1 | 8 | 2 | 8 | 4 | 5 | 9 |
alcune poesie .... per ricordare a memoria le prime 13 cifre del numero di Nepero, la quattordicesima è lo zero.
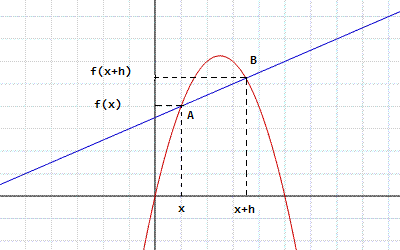
Sia f una funzione definita in un certo intervallo [a,b]. Sia x un punto interno ad [a,b]. Sia h un numero, tale che x+h sia ancora interno ad [a,b].
Si chiama rapporto incrementale della funzione f, nel punto x il numero:
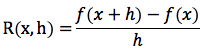
Il simbolo R(x,h) stà a significare proprio che il rapporto incrementale oltre a dipendere dalla funzione f dipende sia dal punto di "partenza" x, che dal tipo di "incremento" h.
In pratica il rapporto incrementale risulta essere il rapporto tra l'incremento delle "y" Δy=f(x+h)-f(x) e l'incremento delle "x" Δx=h.
Considerati nel piano i punti A(x,f(x)) e B(x+h,f(x+h)), il rapporto incrementale corrisponde al coefficiente angolare della retta secante la funzione f(x) passante per A e B.
Defnizione: data una funzione y=f(x), definita nell'intervallo [a,b], ed un punto x la funzione f si dice derivabile nel punto x se esiste finito il limite del rapporto incrementale per h tendente a zero, in simboli:
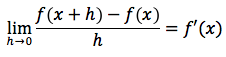
dove h è un numero reale che rappresenta l'incremento della variabile indipendente x.
Il numero reale f'(x) è chiamato derivata della funzione f nel punto di ascissa x.
Una funzione quindi per essere derivabile in un certo punto x, deve avere la derivata destra:
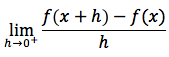
deve avere la derivata sinistra:
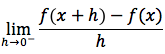
le due derivate devono essere finite e devono essere uguali.
Il valore della derivata f'(x) in un dato punto P, è uguale al coefficiente angolare m della tangente alla curva di equazione y=f(x), nel punto P.
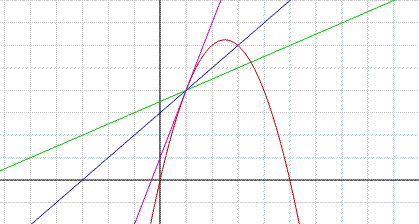
Infatti, come si può notare dalla figura, si sono disegnate due secanti ottenute per due valori di h. Attribuendo ad h valori tendenti a zero i punti nei quali la secante interseca la funzione si "avvicinano".
Quando h diventa uguale a zero la secante corrisponde proprio alla retta tangente la funzione f(x).
Il coefficiente angolare della secante, ovvero il rapporto incrementale della secante, diventa quindi il coefficiente angolare della tangente che corrisponde alla derivata della funzione f(x) nel punto di tangenza.
Sappiamo che la retta di coefficiente angolare m, passante per il punto T(x0;y0) ha equazione:
y-y0=m(x-x0)
sapendo che la derivata di una funzione calcolata in un punto x0 corrisponde al coefficiente angolare della tangente alla curva nel punto (x0;f(x0)), l'equazione della tangente ad una curva y=f(x) nel punto T(x0;f(x0) )è:
y-f(x0)=f'(x0)(x-x0)
Definizione: f si dice derivabile nell'intervallo [a,b] se è derivabile in ogni punto di questo intervallo, in a è sufficiente che ci sia la derivata sinistra, in b la derivata destra. La funzione f' che ad ogni punto x associa f'(x) è detta funzione derivata.
Ipotesi: sia f funzione derivabile in un punto x0
Tesi: la funzione f è continua nel punto x0
Dimostrazione: per ipotesi limx→x0 f(x) = f'(x0) , ovvero esiste ed è finito il limite del rapporto incrementale della f per x che tende ad x0.
Partiamo dall'identità:
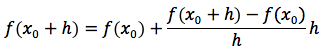
applicando il limite per h tendente a 0 ad entrambi i membri dell'identità otteniamo:
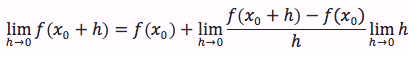
ovvero:
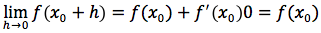
cioè il limite è uguale al valore che la funzione assume nello stesso punto per cui è funzione continua nel punto x0.
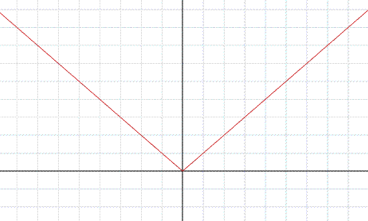
Una funzione continua è derivabile? E' vero cioè il teorema inverso?
Proviamo a dare la risposta al problema analizzando la funzione y=׀x׀.
La funzione nel punto x=0 è continua, infatti la definizione di funzione localmente continua in x=0 è rispettata, anzi la funzione è continua su tutto R.
Vediamo cosa accade ai limiti destro e sinistro del rapporto incrementale:
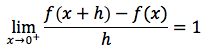
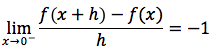
La derivata destra e sinistra esistono, ma non sono uquali. La funzione risulta dunque non derivabile nel punto x=0. Ciò è confermato anche dall'interpretazione geometrica del grafico della curva, infatti a sinistra del punto x=0 la funzione ha per tangente la retta y=-x e a destra dello zero ha per tangente la retta y=x.
Abbiamo trovato così un esempio in cui la condizione di continuità in un punto non è sufficiente affinché la funzione in quel punto sia derivabile e ciò basta per affermare che in generale la condizione di continuità è necessaria , ma non sufficiente perchè la funzione sia derivabile.
Tesi:
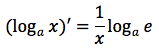
Dimostrazione: Il rapporto incrementale della funzione logaritmo e':
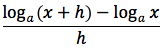
applicando la terza proprieta' del logaritmo possiamo scrivere cosi' il rapporto incrementale:
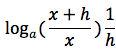
o anche cosi':
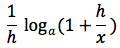
moltiplicando e dividendo per x possiamo scrivere cosi' il rapporto incrementale:
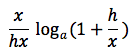
per la quarta proprieta' del logaritmo x/h lo portiamo all'esponente:
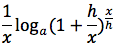
e infine applicando al rapporto incrementale il limite per h tendente a zero otteniamo:
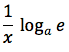
tenendo presente che con "e" si e' indicato il numero di Nepero. Per la proprietà 5 del logaritmo, che in pratica permette di fare un cambiamento di base si può anche scrivere:
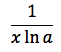
e se la base del logaritmo corrisponde proprio al numero di Nepero la derivata si trasforma in una una relazione molto semplice:
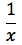
Teorema: la derivata della funzione seno è la funzione coseno
Ipotesi: l'angolo x viene misurato in radiani
Tesi: sin'x=cosx
Dimostrazione: la derivata si otterrà con il limite per h tendente a zero del rapporto incrementale della funzione seno:
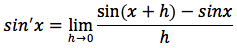
sappiamo che sin(x+h)=sinxcosh+cosxsinh per la formula di addizione del seno quindi possiamo scrivere:
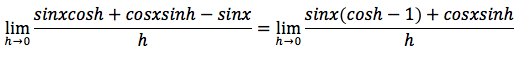
sapendo che il limite di una somma è uguale alla somma dei limiti possiamo scrivere:
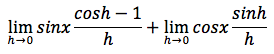
tenendo presente che valgono le seguenti relazioni:
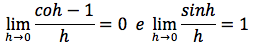
si deduce la tesi:
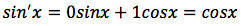
Ipotesi: siano f, g funzioni derivabili
Tesi: la funzione somma f+g è derivabile e si ha: (f+g)'=f'+g'
Dimostrazione: la funzione somma (f+g)(x) è, per definizione, uguale a f(x)+g(x), quindi il rapporto incrementale della g+f è dato da:
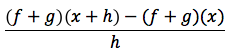
che per definizione può essere scritta anche così:
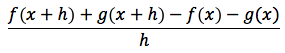
o anche così:
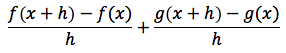
Per ottenere la derivata bisogna passare al limite per h tendente a zero ovvero ci si dovrà ricondurre al limite di una somma che è uguale alla somma dei limiti ovvero:
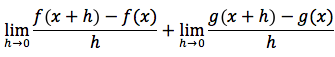
Tenendo conto che il limite del rapporto incrementale della f è f' e che il limite del rapporto incrementale della g è g'otterremo proprio la tesi.
Ipotesi: siano f, g funzioni derivabili
Tesi: la funzione prodotto f*g è derivabile e si ha: (f*g)'=f'*g+f*g'
Dimostrazione: la funzione prodotto (f*g)(x) è, per definizione, uguale a f(x)*g(x), quindi il limite del rapporto incrementale per h tendente a zero della f*g è dato da:
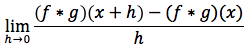
che per definizione è uguale a:
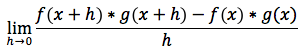
aggiungendo e togliendo dal numeratore il termine: f(x+h)*g(x) otteniamo l'espressione equivalente:
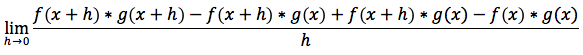
applicando i teoremi sui limiti questa espressione può essere scritta anche così:
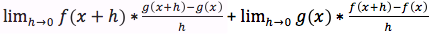
e quindi cosi'
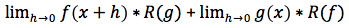
dove, con R(f), R(g) si intendono i rapporti incrementali delle funzioni f e g. Tenendo conto che il limite del prodotto è uguale al prodotto dei limiti, che g(x) e f(x) non dipendono dal tipi di incremento, otterremo proprio la tesi.
Ipotesi: sia k una costante, sia f(x) una funzione derivabile
Tesi: la derivata di kf(x) = kf'(x)
Dimostrazione: applichiamo la formula della derivata di un prodotto: (kf(x))' = k'f(x) + kf'(x), la derivata di una costante k è però uguale a zero e quindi (kf(x))' = kf'(x) c.v.d.
Ipotesi: n sia un numero naturale
Tesi: La derivata di fn è uguale a nfn-1f'.
Dimostrazione: Per dimostrare questo teorema si applicherà il principio di induzione. Il principio consiste nel fatto che, se una proprietà è vera per n=1, supposto sia vera per n-1, se si dimostra che è vera anche per n allora è vera per ogni n appartenente ad N.
si può facilmente verificare che il teorema vale anche per n=1:
Supponiamo ora che la proposizione sia vera per n-1 ovvero (fn-1)'=(n-1)fn-2f' e dimostriamo che è vera per n. Per derivare fn possiamo pensare che fn = fn-1f, quindi per derivare fn applichiamo la formula della derivata di un prodotto:
(fn)' = (fn-1f)' = (fn-1)'f +fn-1f' = (n-1)fn-2f' + fn-1f' = (n-1)fn-1f' + fn-1f' = (n-1+1)fn-1f' = nfn-1f' c.v.d.
Si può dimostrare che la formula è sempre valida anche nel caso in cui n sia un numero negativo o razionale.
Tesi:
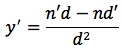
Dimostrazione:
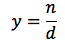
usando la notazione esponenziale si può scrivere:
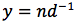
applichiamo la formula della derivata della funzione prodotto:
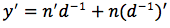
applichiamo la formula della derivata di fn con n=-1:
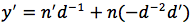
oppure usando la notazione di partenza si può anche scrivere:
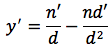
La funzione tangente può essere scritta come rapporto tra seno e coseno:
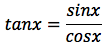
si applica la formula della derivata della funzione rapporto:
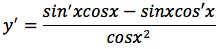
tenendo conto che sin'x=cosx e cos'x=-sinx otteniamo:
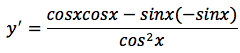
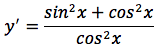
applicando il principio fondamentale della trigonometria: sin2x+cos2x=1, la derivata della funzione tangente può essere scritta in due modi diversi, ma tra loro equivalenti:
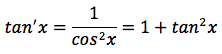
Ipotesi: n sia un numero naturale
Tesi: La derivata di xn è uguale a nxn-1
Proviamo a derivare la funzione x2. Dovremo fare il limite per h tendente a zero del rapporto incrementale della funzione in oggetto. Il rapporto incrementale è:
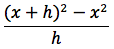
sviluppando otteniamo:
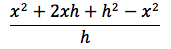
semplificando e raccogliendo il fattore h otteniamo il rapporto incrementale:
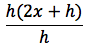
infine semplifichiamo il fattore h e passiamo al limite:
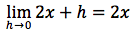
Proviamo ora a derivare la funzione x3. Analogamente al caso precedentemente trattato, dovremmo fare il limite per h tendente a zero del rapporto incrementale della funzione in oggetto. Il rapporto incrementale è:
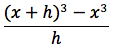
sviluppando otteniamo:
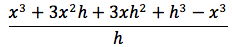
semplificando e raccogliendo il fattore h otteniamo il rapporto incrementale:
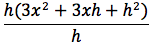
infine semplifichiamo il fattore h e passiamo al limite:
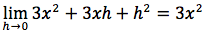
Riassumendo la derivata di x2 è 2x, la derivata di x3 è 3x2. Possiamo quindi prevedere che la derivata di xn sia uguale a nxn-1. c.v.d.
Dimostrazione: Per dimostrare questo teorema si applicherà il principio di induzione. Il principio consiste nel fatto che, se una proprietà è vera per n=1, supposto sia vera per n-1, se si dimostra che è vera anche per n allora è vera per ogni n appartenente ad N.
Gia' abbiamo verificato che il teorema vale per n=2, n=3, verifichiamo che il teorema vale anche per n=1:
Il rapporto incrementale della funzione y = x è:
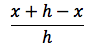
facendo il limite per h tendente a zero troviamo che tale limite è uguale a 1. Quindi si è dimostrato che la derivata della funzione x è 1 e quindi che il teorema è verificato per n=1. Supponiamo ora che la proposizione sia vera per n-1 ovvero (xn-1)'=(n-1)xn-2 e dimostriamo che è vera per n. Per derivare xn possiamo pensare che xn = xn-1x, quindi per derivare xn applichiamo la formula della derivata di un prodotto:
(xn)' = (xn-1x)' = (xn-1)'x + xn-1(x)' = (n-1)xn-2x + xn-11 = (n-1)xn-1 + xn-1 = (n-1+1)xn-1 = nxn-1 c.v.d.
La formula non cambia se n assume valori negativi.
Per esercizio lo verifichiamo nel caso in cui n = - 1, in tal caso il rapporto incrementale è:
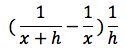
sviluppando si ottiene:
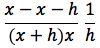
semplificando si ottiene:
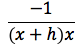
passando al limite per h tendente a zero si ottiene:
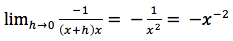
che è proprio quello che si voleva verificare.
La formula rimane tale e quale anche nel caso in cui l'esponente di x sia un numero razionale
Ipotesi: Siano date due funzioni:
w=f(x) f: A→B
y=g(w) g: B→C
supponiamo che, variando x nel dominio A, la funzione w=f(x) assuma valori appartenenti al dominio B della funzione g(w).
Allora le due funzioni date definiscono la funzione composta che possiamo brevemente indicare con y= F(x) cioè poniamo: y=F(x)=g[f(x)]
Tesi: La derivata della funzione F(x) è espressa dalla relazione: F'(x)=f'(x)•g'(w)
Ipotesi: Sia y=f(x) una funzione reale a variabile reale x, continua e invertibile in un intervallo I, derivabile nel punto x ∈ I, con derivata f'(x) ≠ 0. Sia x=fi(y) la sua inversa.
Tesi: fi(y) è derivabile nel punto y=f(x) e si ha: fi'(y) =1/f'(x)
Dimostrazione: Se componiamo la fi(y) con la f(x), risulta: fi[f(x)]=x
derivando entrambi i membri di questa uguagliaza, applicando la regola di derivazione delle funzioni composte si ottiene:
fi'(y) *f'(x) = 1
da questa relazione, essendo per ipotesi f'(x) ≠ 0, si ricava la tesi
La funzione y=fi(x)=arcsinx può scritta come funzione inversa di x=siny, quindi si può applicare la formula della derivata della funzione inversa. Nel primo passaggio la derivata di siny è cosy nel secondo passaggio si è tenuto presente la proprietà fondamentle della trigonometria sin2y+cos2y=1, nell'ultimo passaggio si è tenuto conto che x=siny.
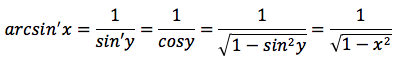
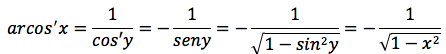
La funzione y=fi(x)=arctanx può scritta come funzione inversa di x=tany, quindi si può applicare la formula della derivata della funzione inversa. Nell'ultimo passaggio si è tenuto conto che x=tany.
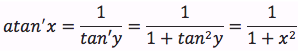
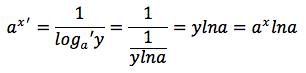
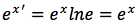
Funzioni crescenti e decrescenti
Sia f(x) una funzione avente per dominio l'intervallo I (che può essere anche illimitato).
Una funzione f(x) è crescente in I se ∀ x1, x2 ∈ I: x1< x2, → f(x1) < f(x2).
Una funzione f(x) è non decrescente in I se ∀ x1, x2 ∈ I: x1< x2, → f(x1) ≤ f(x2).
Una funzione f(x) è decrescente in I se ∀ x1, x2 ∈ I: x1< x2, → f(x1) > f(x2).
Una funzione f(x) è non crescente in I se ∀ x1, x2 ∈ I: x1< x2, → f(x1) ≥ f(x2).
Concavità, convessità, flessi
Una curva è concava in un punto x0 ovvero ha la concavità rivolta verso il basso se esiste un intorno di x0 in cui i punti del grafico stanno al di sotto della tangente in x0 (escluso x0)
Una curva ha la concavità rivolta verso l'alto in un punto x0 ovvero é convessa se esiste un intorno di x0 in cui i punti del grafico stanno al di sopra della tangente in x0 (escluso x0)
Se la tangente invece attraversa la funzione nel punto x0 si dice che la curva ha un punto di flesso in x0
Massimi e minimi assoluti e relativi
Sia f(x) una funzione avente per dominio l'intervallo chiuso [a,b], sia x0 ∈ [a,b].
x0 è punto di massimo assoluto per f(x) se ∀ x ∈ [a,b] risulti: f(x)≤f(x0)
x0 è punto di minimo assoluto per f(x) se ∀ x ∈ [a,b] risulti: f(x)≥f(x0)
x0 è punto di massimo relativo per f(x) se ∃ un intorno U (U⊂[a,b]) di x0: ∀ x ∈ U risulti: f(x)≤f(x0)
x0 è punto di minimo relativo per f(x) se ∃ un intorno U (U⊂[a,b]) di x0: ∀ x ∈ U risulti: f(x)≥f(x0)
ipotesi: f(x) continua in I, f'(x)>0 ∀x∈I
tesi: f(x) è crescente in I
ipotesi: f(x) continua in I, f'(x)<0 ∀x∈I
tesi: f(x) è decrescente in I
ipotesi: f(x) continua in I, derivabile in I, x0, interno ad I, sia massimo (o minimo) relativo
tesi: f'(x0)=0
ipotesi: sia f(x) definita in I, continua, con derivata prima e seconda in un intorno U di x0, interno ad I, sia f''(x0)>0
tesi: La concavità è rivolta verso l'alto
ipotesi: sia f(x) definita in I, continua, con derivata prima e seconda in un intorno U di x0, interno ad I, sia f''(x0)<0
tesi: La concavità è rivolta verso il basso
ipotesi: sia f(x) definita in I, continua, con derivata prima e seconda in un intorno U di x0, interno ad I, sia f''(x0)=0, la prima derivata, dopo la seconda che non si annulla è di ordine dispari (ovvero se f'''(x0)≠0 fv(x0)≠0....)
tesi: x0 è punto di flesso.
Data una curva mediante la sua equazione cartesiana y=f(x), per disegnarne il grafico e determinandone le principali proprietà, procediamo ad analizzare i seguenti punti:
Per quanto riguarda il dominio o campo di esistenza, se non viene assegnato, bisogna calcolarlo in base all'espressione analitica della funzione stessa. Questa espressione analitica può contenere operazioni come somma, prodotto, quoziente, radici, potenze, logaritmi .... e quindi occorre determinare l'insieme dei numeri reali per i quali hanno senso tutte le operazioni (o funzioni) presenti.
Per studiare il segno della funzione, cioè per valutare quando la funzione è positiva o negativa bisogna determinare quali sono i valori della x appartenenti al dominio che soddisfano le disequazioni f(x)>0, f(x)<0. A questo punto conviene tratteggiare sul piano cartesiano tutte le zone in cui non si sviluppa il grafico della funzione, se ad esempio nell'intervallo [a,b] la funzione risultasse positiva si tratteggia la zona del piano sotto l'asse x.
Si possono presentarsi i seguenti tipi di simmetrie. Se ∀ x ∈ dominio, f(x)=f(-x), allora la funzione è simmetrica rispetto all'asse y, in questo caso si dice che la funzione è pari. Per disegnarne il grafico sarà sufficiente studiare la funzione nel primo e quarto quadrante, per poi ruotare il grafico intorno all'asse y, facendo quindi corrispondere ad ascisse opposte la stessa ordinata. Se ∀ x ∈ dominio, f(-x)=-f(x), allora la funzione è simmetrica rispetto all'origine degli assi, in tal caso si dice che la funzione è dispari. Sarà sufficiente disegnare il grafico della funzione nel primo e quarto quadrante, per poi attraverso una simmetria centrata nell'origine riportare il grafico nel terzo e quarto quadrante, facendo corrispondere ad ascisse opposte, ordinate opposte.
Se si verifica che f(x)=f(x+P) ∀ x ∈ dominio allora si dirà che una funzione sia periodica di un certo periodo P, in tal caso sarà sufficiente studiare la funzione nell'intervallo chiuso [0,P], per poi ricopiare il grafico in tutti gli intervalli desiderati [ kP,kP+P ] con k∈N.
Una curva è detta asintoto di una funzione se la distanza di un punto della funzione dalla curva tende a zero quando l'ascissa o l'ordinata del punto tendono all'infinito. Se la curva è una retta orizzontale, l'asintoto si dirà asintoto orizzontale. Se la curva è una retta verticale, l'asintoto si dirà asintoto verticale. Se la curva è una retta obliqua, l'asintoto si dirà asintoto obliquo. Se la curva è una parabola, l'asintoto si dirà parabola asintotica.
Per determinare l'andamento della funzione occorre calcolare i limiti negli estremi del campo di esistenza, più precisamente se D è l'unione di un numero finito di intervalli disgiunti I1, I2 ..... In, si tratta di calcolare i valori che la funzione assume negli estremi di I1, I2 ..... In e se la funzione non è definita in questi estremi vedere se esiste il limite, calcolandone il valore quando x tende a questi estremi.
Vista la definizione, una funzione risulta continua in x0 dove assume il valore finito f(x0) se valgono queste tre condizioni:
1. esiste limite destro finito per x tendente ad x0
2. esiste limite sinistro finito per x tendente ad x0
3. Il limite destro è uguale al limite sinistro ed è uguale a f(x0)
Una funzione è discontinua in un punto se in quel punto viene meno una delle tre condizioni per la continuità.
Discontinuità di primo tipo: se il limite sx è diverso da quello dx e sono entrambi finiti, allora la discontinuità sarà di primo tipo e la differenza in valore assoluto tra i 2 limiti si dirà salto della funzione
Discontinuità di secondo tipo: se uno dei 2 limiti (DX o SX) non esiste o è infinito allora la discontinuità sarà di secondo tipo.
Discontinuità di terzo tipo: quando il valore assunto dalla funzione è diverso dal limite oppure quando c'è un "buco" ovvero non esiste la funzione in quel punto.
Può essere utile, individuare alcuni punti del piano che appartengono al grafico della funzione, in particolare le eventuali intersezioni con gli assi cartesiani. Per individuare le intersezioni con l'asse x bisogna risolvere l'equazione f(x) = 0. Risolvendo l'equazione, si possono presentare i seguenti casi: o l'equazione non ha soluzioni allora il grafico della funzione non interseca l'asse x; oppure l'equazione presenta un numero finito di soluzioni in questo caso il grafico ha un numero finito di punti di intersezione con l'asse x; oppure ancora l'equazione ha infinite soluzioni per cui il grafico della funzione ha infiniti punti di intersezione con l'asse x. Per quanto riguarda invece l'eventuale intersezione con l'asse y, esiste ed è unica solamente se lo zero appartiene al dominio della funzione. Questo perchè, per definizione di funzione, su ogni verticale può starci al massimo un punto. Basterà quindi sostituire a x il valore zero e la eventuale soluzione sarà il punto di coordinate (0,f(0)).
Per avere un'indicazione precisa sull'andamento del grafico sarà la determinazione degli intervalli dove la funzione risulta crescente o decrescente. Se la funzione sarà derivabile sarà il segno della derivata a dirci esattamente come si comporterà la funzione da questo punto di vista. Più precisamente la f sarà crescente negli intervalli dove la f' sarà positiva e decrescente in quelli dove f' sarà negativa. Per questo motivo si dovrà studiare l'equazione f'(x)=0 che sarà pure importante per la ricerca dei punti di massimo e minimo relativi, concavità e flessi.
A questo punto bisogna fare un riepilogo delle informazioni ottenute, magari completandole con qualche nuova osservazione. E' importante avere una conoscenza globale sul comportamento di una funzione, perché ciò ci potrà permettere di fare delle verifiche su dei calcoli già compiuti. Se per esempio un certo limite in x0 assumesse un valore positivo, ma lo studio del segno ci dicesse che in x0 la funzione assume un valore negativo sarebbe evidente che qualche calcolo non è stato fatto in modo corretto e che quindi si deve procedere a trovare gli errori.
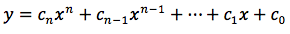
Una funzione razionale è di questo tipo:
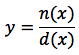
dove n e d sono rispettivamente due polinomi, più precisamente può essere scritta così:
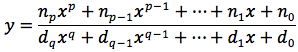
dove ni e di sono rispettivamente i coefficienti del numeratore e del denominatore, p e q rispettivamente i gradi del numeratore e del denominatore.
Per determinare il dominio o campo di esistenza della funzione, bisogna escludere i valori nei quali si annulla il denominatore
Studio del segno: risolvendo la disequazione f(x)>0 si troveranno gli eventuali intervalli dove la funzione stessa risulterà positiva, la funzione risulterà negativa nell'insieme complementare.
Asintoti: In ogni punto dove si annulla il denominatore ci sarà un asintoto verticale a meno che in quel punto non si annulli pure il numeratore, in quest'ultimo caso potrebbe esserci un cosìdetto punto di discontinuità di terza specie, dal punto di vista grafico un "buco" della funzione. La funzione razionale f(x) si presenta come rapporto di due polinomi f(x)=n(x)/d(x). Se eseguiamo la divisione tra numeratore e denominatore troviamo un certo quoziente q(x) ed un certo resto r(x). Il grado del quoziente sarà: grado(q) = grado(n) - grado(d), il grado del resto dovrà minore del grado del denominatore d. A questo punto potremo scrivere che n:d=q, con resto r e di conseguenza n=qd+r. Dividendo entrambi i membri dell'ultima relazione scritta per d otteniamo: n/d=(qd+r)/d o anche n/d=q+r/d. In altre parole la nostra funzione razionale può essere scritta come somma del quoziente con l'altra funzione razionale r/d. Tenendo presente che in r/d il grado di r è minore del grado di d, il limite per x tendente all'infinito sarà uguale zero. A questo punto possiamo pensare che per x tendente ad infinito, la funzione razionale n/d tende a q, q allora sarà per definizione l'asintoto di n/d. Quindi se q è di grado zero ed è zero ci sarà un asintoto corrispondente all'asse delle ascisse, se q è di grado zero ma è un numero diverso da zero, ci sarà un asintoto orizzontale non coincidente all'asse delle ascisse, se q è di grado uno ci sarà per asintoto una retta obliqua, se q è di grado due ci sarà una parabola asintotica ecc... ecc... Quindi se, per esempio, il grado del numeratore è tre ed il grado del denominatore è due, la differenza dei gradi tra numeratore e denominatore è uno. Uno sarà quindi il grado dell'asintoto e quindi la funzione razionale avrà per asintoto una retta obliqua.
Limiti: si dovranno calcolare i limiti per x tendente a più infinito e meno infinito per capire come si comporta la funzione in questi due casi e i limiti dovranno confermare quello che si è calcolato nel punto precedente riguardante gli asintoti. Dovranno essere calcolati quindi i limiti per x tendente ai punti nei quali la funzione non è definita e queti limiti dovranno confermare quello quello che si è ottenuto calcolando gli asintoti verticali.
Mettendo a sistema l'equazione della funzione, con l'equazione degli assi: (y=0 asse ascisse, x=0 asse delle ordinate) e risolvendo i due sistemi si otterranno gli eventuali punti di intersezione della funzione con gli assi.
Attraverso lo studio della derivata sarà possibile individuare gli eventuali intervalli dove la funzione risulta crescente o decrescente, se ci saranno punti di massimo minimo o flesso.
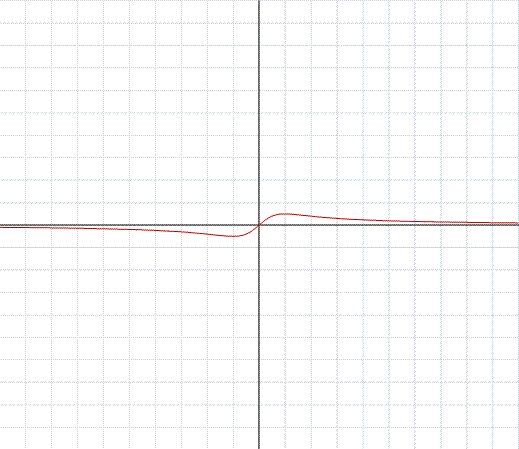
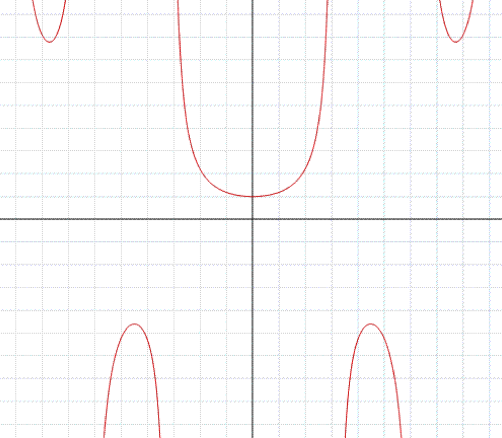
Nell'esempio in figura, troviamo il grafico della funzione razionale:
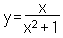
Notiamo che il numeratore è di primo grado e il denominatore di secondo.
Eseguendo la divisione tra numeratore e denominatore troviamo che il quoziente è zero appunto perchè il grado del denominatore è maggiore del grado del numeratore.
Il quoziente della divisione è l'asintoto della funzione, in questo esempio quindi l'asintoto è la retta y=0 che corrisponde, come si nota dal grafico, all'asse delle ascisse.
Si noti ancora che la funzione è definita per ogni valore reale, questo perchè il denominatore non si annulla per alcun valore reale.
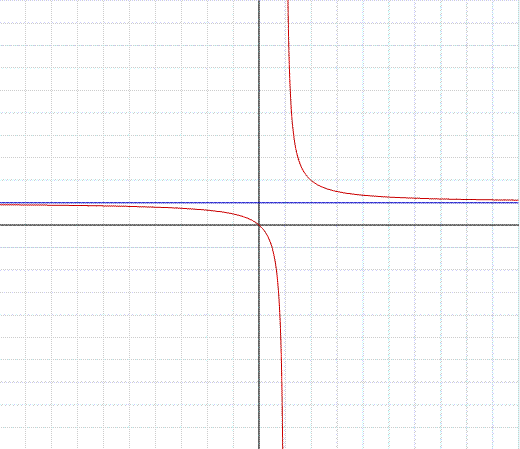
Nell'esempio in figura, troviamo il grafico della funzione razionale:
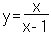
Notiamo che sia il numeratore che il denominatore sono di primo grado.
Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di grado zero,
che in pratica è il numero ottenuto dividendo i coefficienti n1/d1
che nello specifico corrisponde al numero 1.
y=1 è l'asintoto della funzione, quindi
asintoto orizzontale.
Si tenga conto che la funzione ha pure un asintoto verticale x=1 nel
punto dove si annulla il denominatore.
Il punto 1 è un punto di discontinuità di seconda specie.
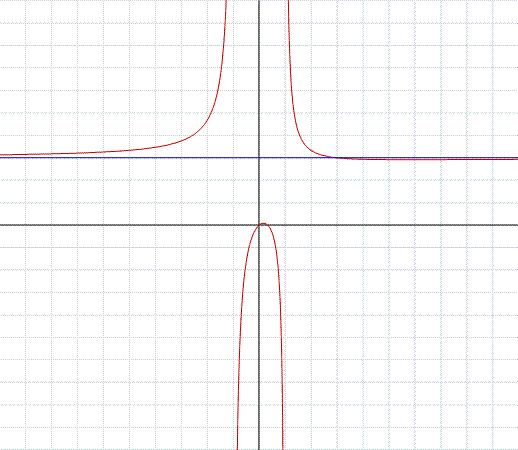
Nell'esempio in figura, troviamo il grafico della funzione razionale:
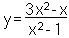
Notiamo che sia numeratore che il denominatore sono di secondo grado.
Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di grado zero, che in pratica è il numero ottenuto dividendo i coefficienti n2/d2 e nello specifico corrisponde al numero 3.
y=3 è l'asintoto della funzione, quindi asintoto orizzontale.
Si noti ancora che la funzione
ha pure gli asintoti verticali x=1 x=-1, nei punti dove si annulla il denominatore.
I punti 1 e -1 sono punti di discontinuità di seconda specie.
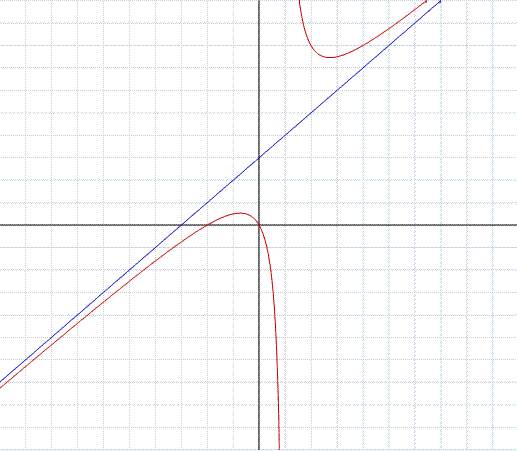
Nell'esempio in figura, troviamo il grafico della funzione razionale:
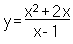
notiamo che il numeratore è di secondo grado e il denominatore di primo.
Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di primo grado, esattamente: x+3
y=x+3 è l'asintoto della funzione, quindi asintoto obliquo.
Si noti ancora che la funzione ha pure l'asintoto verticale x=1 nel punto dove si annulla il denominatore.
Il punto 1 è un punto di discontinuità di seconda specie.
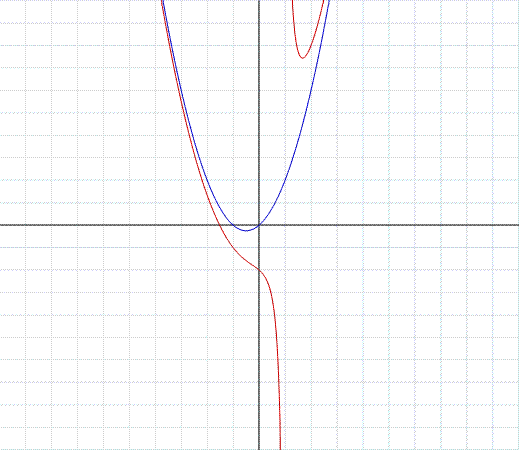
nell'esempio in figura, troviamo il grafico della funzione razionale:
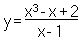
notiamo che il numeratore è di terzo grado e il denominatore di primo. Eseguendo la divisione tra numeratore e denominatore troviamo questo quoziente di secondo grado, di colore blu in figura:
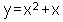
Il quoziente della divisione è l'asintoto della funzione, che chiameremo parabola asintotica.
Si noti ancora che la funzione ha pure l'asintoto verticale x=1 nel punto dove si annulla il denominatore.
Il punto 1 è un punto di discontinuità di seconda specie
Una funzione si dice irrazionale se nella relativa espressione analitica, la variabile indipendente x sta "sotto" ad una radice. Analizzeremo, in particolare, funzioni irrazionali di questo tipo:
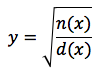
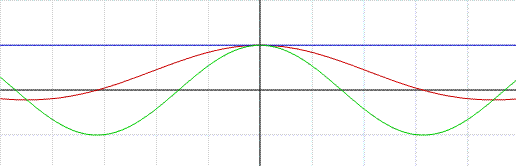
ovvero si tratta di una funzione razionale posta all'interno di una radice quadrata. Supponiamo di conoscere il grafico di questa funzione razionale e cerchiamo di valutare come una radice quadrata può "modificarlo".
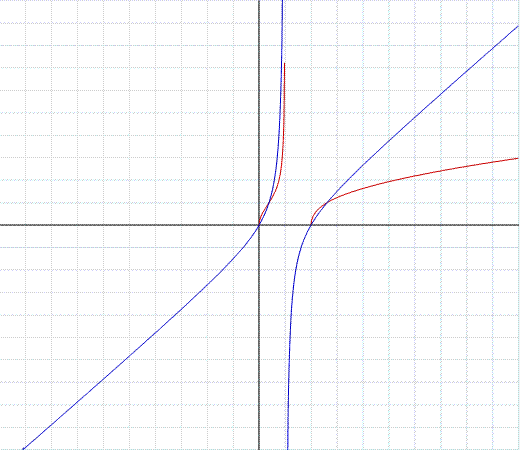
Nel primo grafico sono messe a confronto la funzione:
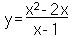
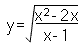
Sono messe a confronto, quindi due funzioni che "differiscono" per una radice quadrata.
Teniamo presente che una radice quadrata è impossibile in R quando l'argomento della radice stessa assume valori negativi.
Ne consegue che, dove la funzione razionale è negativa, la funzione irrazionale non ha dominio.
La funzione irrazionale, del tipo considerato, si sviluppa quindi solamente sopra l'asse x ovvero nel primo e secondo quadrante.
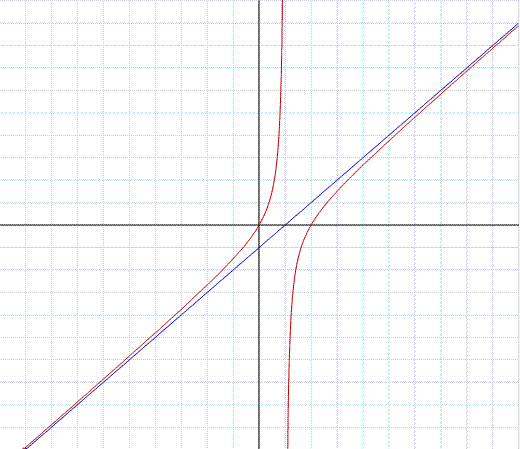
Notiamo ancora che: la radice quadrata "cala" i valori maggiori di 1, e "solleva" i valori minori di 1, lascia inalterato il valore 1.
Tutto ciò lo si può verificare sul grafico, in quanto l'orizzontale y=1 interseca entrambe le funzioni mentre sopra la retta y=1 la funzione irrazionale in nero "cala" rispetto alla funzione razionale in blu, sotto la retta y=1 la funzione irrazionale si "solleva" rispetto alla funzione razionale. Infatti la radice di 4 "cala" e diventa 2, perchè 4 è un numero maggiore di 1, la radice di 0,49 si "solleva" a 0,7 infatti 0,49 è un numero minore di 1. La radice di 1 rimane sempre 1.
Si noti, nel secondo grafico, che la funzione:
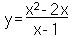
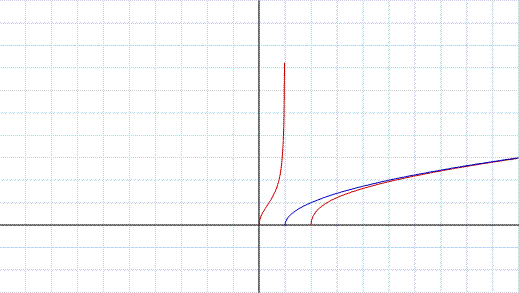
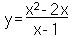
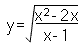
(in nero in figura) ha per asintoto la curva:
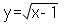
(in blu in figura).
Il concetto di derivata fu proposto nel secolo XVII da Fermat. Nello stesso secolo diversi altri matematici tra cui Mengoli e Cavalieri dell'università di Bologna, diedero un grande contributo allo sviluppo del concetto di integrale. Il teorema fondamentale del calcolo integrale, va tuttavia sotto il nome di Torricelli - Barrow, infatti, sia Torricelli (1608-47), che fu discepolo di Galileo, sia Barrow (1603-77), che fu maestro di Isaac Newton, contribuirono alla sua dimostrazione. Si deve però a Newton (1642-1727) e Leibnitz (1646-1716) il merito di aver trovato la stretta relazione tra i concetti di derivata ed integrale. Storicamente l'integrale definito risolse il problema del calcolo di aree delimitate da curve.
Se f(x) è una funzione [a,b]→R continua e positiva ovvero se f(x) ≥ 0, ∀ x ∈ [a,b], si consideri l'area compresa tra questa funzione e le rette y=0, x=a, x=b. Quest'area si chiama trapezoide. Ci proponiamo di dare una definizione di ciò che si intende per area del trapeziode. Dividiamo l'intervallo [a,b] in n intervallini di varia misura indicando con h1, h2 ....hn, le ampiezze di questi intervallini. Prendiamo ad arbitrio nel primo intervallino un punto w1, nel secondo un punto w2, e...nell'ennesimo intervallino un punto wn, e calcoliamo quindi i corrispondenti valori della funzione f(w1), f(w2) ... f(wn). Si arriva così a costruire una famiglia di rettangolini che chiameremo plurirettangolo.
Ipotesi: f(x) sia una funzione [a,b]→R continua
Tesi: esiste ed è finito il seguente limite:
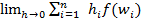
dove h è la massima ampiezza degli intervallini h1, h2 ....hn
Si chiama integrale definito della funzione continua f(x): [a,b]→R il numero che rappresenta il limite per h→0 della successione:
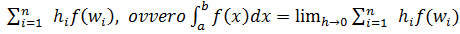
Il valore di questo limite esiste ed ha sempre lo stesso valore comunque si faccia tendere a zero l'ampiezza degli intervallini in cui si suddivide l'intervallo [a,b], e comunque si prendano i punti wi negli intervallini stessi. L'area del trapezoide, per definizione, è proprio uguale al numero determinato da questo limite, hi rappresenta la base e f(wi) l'altezza del singolo rettangolino in cui è suddiviso il trapezoide.
1. Se a è minore di b, si pone per definizione
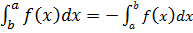
in questo modo si attribuisce un significato all'integrale definito anche quando l'estremo inferiore è maggiore dell'estremo inferiore.
2. Si pone per definizione
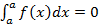
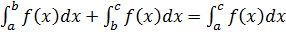
2. Teorema della scomposizione. Se f(x), g(x) .. q(x) sono funzioni continue nell'intervallo [a,b] si ha:
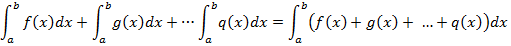
3. Se f(x) è continua in un intervallo [a,c] e k è una costante allora
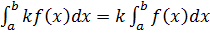
L'integrale definito di una funzione continua f(x) è uguale alla misura dell'intervallo di integrazione [a,b] moltiplicata per il valore che la funzione integranda assume per un opportuno valore w di [a,b]. In altre parole il teorema della media dice che l'area del trapezoide delimitato dalle rette y=0, x=a, x=b e dalla funzione f(x), equivale all'area di un rettangolo che ha per base la stessa base [a,b] e per altezza f(w) dove w è un opportuno valore di [a,b]. La retta orizzontale y=f(w), viene anche detta retta di compenso.
Sia f(x) una funzione [a,b]→R continua e positiva f(x) ≥ 0, x ∈ [a,b] L'integrale definito
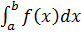
è un preciso numero reale che dipende dagli estremi di integrazione a e b. Supponendo variabile l'estremo superiore che chiameremo x, allora la funzione
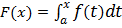
è una funzione dell'estremo superiore x. Come si sarà già notato, per evitare confusione tra la variabile x, della funzione f, e l'estremo superiore x di integrazione, si è sostituito alla variabile x la variabile t. La funzione F(x) si chiama funzione integrale, la f(t) si chiama funzione integranda.
Ipotesi: Sia f(x) una funzione [a,b]→R continua e positiva f(x) ≥ 0, x ∈[a,b].
Tesi: esiste la derivata della funzione integrale nel punto x ed è uguale al valore che la funzione integranda assume nello stesso punto x, ovvero: F'(x) = f(x).
Dimostrazione: bisogna valutare il limite del rapporto incrementale della funzione integrale per h→0: partiamo dal rapporto incrementale della F:
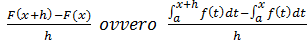
e in base alla proprietà additiva potremo scrivere:
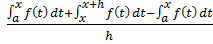
e semplificando:
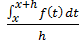
applicando al numeratore il teorema della media, esisterà un w compreso tra [x,x+h] tale che
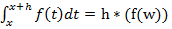
quindi sostituendo:
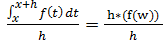
e semplificando h:
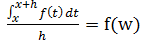
ovvero potremo concludere che il rapporto incrementale della F è uguale a f(w) con w un opportuno valore compreso tra [x,x+h]. Facendo il limite per h tendente a 0, tenendo conto della continuità della f, questo limite sarà uguale a f(x) ovvero:
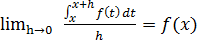
ovvero F'(x)=f(x) che è quanto si voleva dimostrare.
Definizione: se p(x) è una funzione che in ogni punto di un intervallo [a,b] abbia per derivata f(x), si dice che P(x) è una primitiva di f(x), ovvero P'(x) = f(x).
La famiglia delle primitive di una funzione f(x) si chiama integrale indefinito della f(x) e si indica con il simbolo:
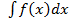
come si può notare nel simbolo dell'integrale indefinito non sono previsti gli estremi di integrazione. Si parla di "famiglia delle primitive" poiché se p(x) è primitiva di f(x), pure p(x) + k è primitiva di f(x), dove con k si è indicato un qualunque valore reale. Data una funzione e gli estremi di integrazione, l'integrale definito restituisce quindi un numero, che rappresenta un'area. L'integrale indefinito invece data una funzione mi restituisce una famiglia di funzioni ovvero la famiglia delle primitive, in altre parole l'operazione di integrazione indefinita può essere considerata come operazione inversa della derivazione.
Esempio
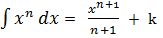
Infatti calcolando la derivata di x(n+1)/(n+1) + k , si ottiene proprio xn.
Supponiamo che P(x) sia una delle primitive di f(x), quindi avremo: P'(x) = f(x) e siccome per il teorema fondamentale si è dimostrato che risulta anche F'(x)=f(x) si può dire che P(x), F(x) differiscono per una costante ovvero: P(x) = F(x) + k ossia
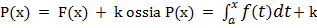
Se si pone x=a risulta:
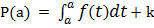
Tenendo presente che l'integrale che va da a in a è uguale a zero (seconda proprietà) si ottiene che P(a) = k. Sostituendo si ottiene:
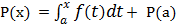
In quest'ultima relazione ponendo x = b e trasportando P(a) al primo membro si ottiene:
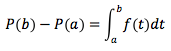
Questa è proprio la formula per il calcolo delle aree e si scrive anche
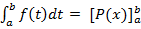
Questa semplice formula permette di superare le difficoltà di calcolare un'area con il limite per h→0 della sommatoria dei plurirettangoli, limite che è molto difficile da determinarsi, ricalcando un percorso fatto in laboratorio con l'ausilio del foglio elettronico per il calcolo di un'area dove f(x) è una semplice parabola.
Sia f(x) una funzione [a,b]→R continua e positiva ovvero se f(x) ≥ 0, ∀ x ∈ [a,b], si consideri il trapezoide delimitato da questa funzione e le rette y=0, x=a, x=b. Questo trapezoide, ruotando di un giro attorno all'asse x, genera un solido del quale vogliamo definire e calcolare il volume. A questo scopo dividiamo l'intervallo [a,b] in n intervallini di varia misura indicando con h1, h2, ....hn, le ampiezze di questi intervallini. Prendiamo ad arbitrio nel primo intervallino un punto w1, nel secondo un punto w2, e...nell'ennesimo intervallino un punto wn, e calcoliamo quindi i corrispondenti valori della funzione f(w1), f(w2) .. f(wn). Ruotando di un giro completo attorno all'asse x, il plurirettangolo descrive un solido che è l'insieme di n cilindretti aventi per base i cerchi i cui raggi sono i valori f(wi) e per altezza gli intervallini in cui è stato suddiviso [a,b]. Il volume dell'i-esimo cilindretto si calcola quindi πhf2 (wi,) ed il volume del pluricilindro è dato da:
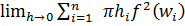
abbiamo quindi che il volume V del solido di rotazione è dato da:
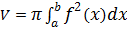
Sia f(x) una funzione [a,b]→R continua e positiva ovvero se f(x) ≥ 0, ∀ x ∈ [a,b], si consideri il trapezoide delimitato da questa funzione e le rette y=0, x=a, x=b. Questo trapezoide, ruotando di un giro attorno all'asse x, genera un solido del quale vogliamo definire e calcolare il volume. A questo scopo dividiamo l'intervallo [a,b] in n intervallini di varia misura indicando con h1, h2, ....hn, le ampiezze di questi intervallini. Prendiamo ad arbitrio nel primo intervallino un punto w1, nel secondo un punto w2, e...nell'ennesimo intervallino un punto wn, e calcoliamo quindi i corrispondenti valori della funzione f(w1), f(w2) .. f(wn). Ruotando di un giro completo attorno all'asse x, il plurirettangolo descrive un solido che è l'insieme di n cilindretti aventi per base i cerchi i cui raggi sono i valori f(wi) e per altezza gli intervallini in cui è stato suddiviso [a,b]. Il volume dell'i-esimo cilindretto si calcola quindi πhf2 (wi,) ed il volume del pluricilindro è dato da:
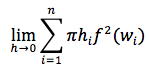
Il volume V del solido di rotazione è quindi dato da:
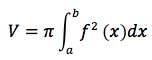
Volume della sfera
Pensiamo che la sfera sia generata dalla rotazione attorno all'asse x del semicerchio avente centro nell'origine e raggio r. L'equazione della circonferenza è: x2+y2= r2 ovvero y2= r2-x2. In base alla formula quindi il volume della sfera è:
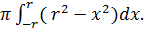
Per rendere i calcoli più semplici potremo, vista la simmetria della sfera calcolare il volume della semisfera:
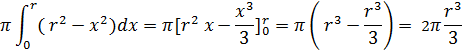
raddoppiando il volume ottenuto troveremo quindi il volume delle sfera:
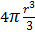
Volume del cono
Il volume del cono di altezza h ottenuto da una rotazione intorno all'asse x della bisettrice y=x si ottiene:
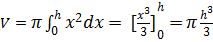
Volume del trono di cono
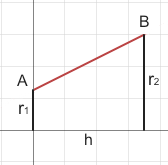
Nella figura di sinistra ruotando intorno all'asse delle ascisse la retta che passa per i punti A(0,r1) e B(h,r2) otteniamo un tronco di cono di altezza h e le basi rispettivamente di raggi r1 e r2. Il coefficiente angolare m, della retta e l'equazione della retta stessa sono indicati nelle figure a destra.
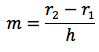
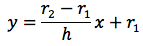
Per ottenere il volume del tronco di cono bisognerà risolvere quindi il seguente integrale:
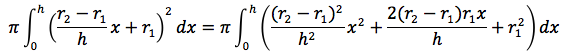
Si ottiene:
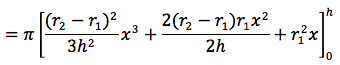
Facendo il minimo comune multiplo si ottiene:
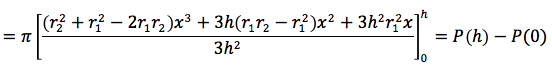
Calcoliamo P(h) e P(0):
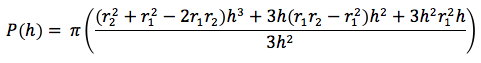
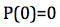
Raccogliendo h, il volume sarà quindi dato da:
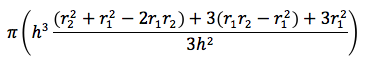
semplificando il denominatore si ottiene:
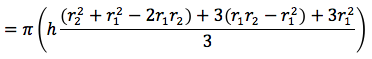
semplificando ulteriormente si ottiene:
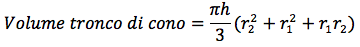
Definizione: se P(x) è una funzione che in ogni punto di un intervallo [a,b] abbia per derivata f(x), si dice che P(x) è una primitiva di f(x), ovvero P'(x) = f(x).
La famiglia delle primitive di una funzione f(x) si chiama integrale indefinito della f(x) e si indica con il simbolo:
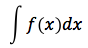
Come si può notare nel simbolo dell'integrale indefinito non sono previsti gli estremi di integrazione. Si parla di "famiglia delle primitive" poiché se p(x) è primitiva di f(x), pure p(x) + k è primitiva di f(x), dove con k si è indicato un qualunque valore reale. Data una funzione e gli estremi di integrazione, l'integrale definito restituisce quindi un numero, che rappresenta un'area. L'integrale indefinito invece data una funzione mi restituisce una famiglia di funzioni ovvero la famiglia delle primitive, in altre parole l'operazione di integrazione indefinita può essere considerata come operazione inversa della derivazione.
Nelle formule scritte di seguito l'integrale si determina in modo immediato ottenendo come primitiva una funzione elementare. Per verificare la validità delle formule è sufficiente derivare la primitiva per ottenere la funzione integranda.
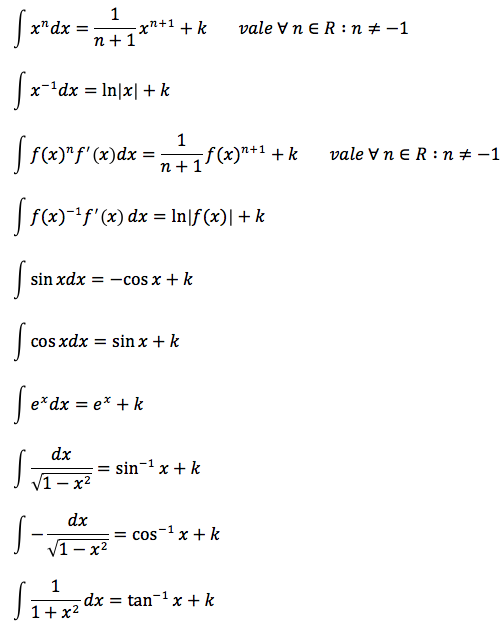
E' una regola che consente, sotto la condizione che la funzione integranda sia scomponibile nel prodotto di due funzioni, di calcolare l%u2019integrale assegnato in termini di un altro integrale. Supponiamo di avere due funzioni f e g derivabili. Applicando la formula della derivata di un prodotto si ottiene:
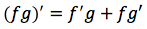
Integrando sia il primo che il secondo termine si ottiene:
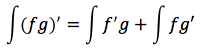
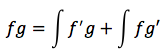
Per ottenere la formula finale:
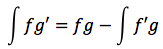
Si possono stabilire due regole generali:
La parte scelta come f' dev'essere facilmente integrabile.
L'integrale che compare al secondo termine dev'essere integrabile più facilmente di quello di partenza.
Una funzione razionale è una funzione di questo tipo:
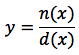
dove n e d sono rispettivamente due polinomi, più precisamente può essere scritta così:
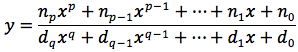
dove ni e di sono rispettivamente i coefficienti del numeratore e del denominatore, p e q rispettivamente i gradi del numeratore e del denominatore.
Se il grado di n(x) è maggiore o uguale al grado di d(x) si esegue la divisione tra numeratore e denominatore. Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente q(x) ed un resto r(x). Il grado del quoziente sarà: grado(q) = grado(n) - grado(d), il grado del resto dovrà essere minore del grado del denominatore d. A questo punto potremo scrivere che n:d=q, con resto r e di conseguenza n=qd+r. Dividendo entrambi i membri dell'ultima relazione scritta per d otteniamo: n/d=(qd+r)/d o anche n/d=q+r/d. In altre parole la nostra funzione razionale può essere scritta come somma del quoziente con l'altra funzione razionale r/d. Tenendo presente che in r/d il grado di r è minore del grado di d. Scrivendo la funzione razionale in questo modo, potremmo scomporre l'integrale in una somma di due integrali:
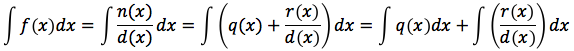
Il primo dei due integrali è immediato in quanto la funzione integranda è un semplice polinomio. Il problema ora diventa quello di calcolare l'integrale di una funzione razionale in cui il grado del denominatore supera il grado del numeratore. Per limitarci a considerare alcuni semplici casi pensiamo che il denominatore sia di secondo grado quindi d(x)=ax2+bx+c e vediamo come procedere nel caso in cui il discriminante sia maggiore di zero oppure sia uguale a zero. Poniamo che il discriminante sia maggiore di zero, l'equazione associata al denominatore avrà due soluzioni distinte x1 e x2, d(x) si potrà così scomporre d(x)=(x-x1)(x-x2) e la funzione da integrare potrà essere scritta:
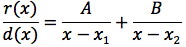
quindi
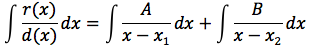
a questo punto impostando un semplice sistema si ricavano A e B e quindi ci si riconduce a risolvere due integrali immediati, si ottiene quindi:
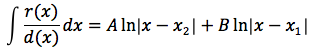
Poniamo che il discriminante sia uguale a zero, l'equazione associata al denominatore avrà una soluzione x0 d(x) si potrà così scomporre d(x)=(x-x1)(x-x1) e la funzione da integrare potrà essere scritta:
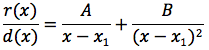
come in precedenza, impostando un semplice sistema si ricavano A e B e quindi ci si riconduce a risolvere due integrali immediati
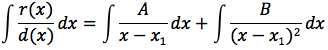
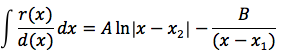
La funzione integranda sia y=f(x), f: A→B, poniamo che F sia una primitiva di f, y=F(x) F: A→B, quindi F'=f. Per rendere il calcolo dell'integrale più semplice, a volte conviene eseguire una sostituzione il che equivale a considerare una funzione x=g(t) g: C→A, il cui codominio sia incluso nel dominio di f. In questo modo si può pensare che la f sia una funzione composta f(g(t)) f: C→B. Essendo anche F definita in A, ha senso considerare anche F come funzione composta ovvero y=F(g(t)).
Per la regola di derivazione delle funzioni composte risulta: (F(g(t)))'=F'(g(t))g'(t) ovvero (F(g(t)))'=f(g(t))g'(t). Esequendo l'integrale sia del primo che del secondo termine della precedente uguaglianza si trova:
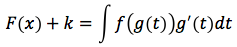
Nel caso in cui si dovesse calcolare l'integrale definito tra x1 e x2, vanno modificati gli estremi di integrazione tenendo presente che la variabile t viene calcolata dalla seguente funzione: t=g-1(x). I nuovi estremi di integrazione saranno t1 e t2 con t1=g-1(x1) e t2=g-1(x2), dunque: