Risoluzione triangoli rettangoli
Negli esercizi che seguono si faccia riferimento ad un triangolo di questo tipo:
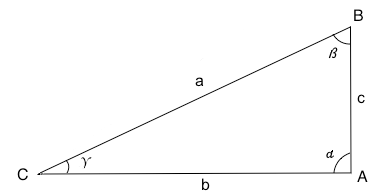
Risolvere un triangolo rettangolo ABC con angolo retto in A dati i due cateti b=5 c=12
Si potrebbe determinare l'ipotenusa applicando il teorema di Pitagora, si consiglia di applicare le formule della trigonometria per far pratica sulle stesse, riservando il teorema di Pitagora per l'eventuale verifica.
Conoscendo i due cateti possiamo sfruttare la seguente formula: tanβ=b/c. In tale formula c'è un' unica incognita, l'angolo β che ricaviamo β=tan-1(b/c), ovvero sostituendo: β=tan-1(5/12)=22°37'12''. L'angolo γ si può calcolare in modo analogo: γ=tan-1(c/b) ovvero γ=tan-1(12/5)=67°22'48''. Se i calcoli sono esatti β+γ=90°. L'ipotenusa si può trovare con la seguente formula: a=b/sinβ=5/sin(22°37'12'')=13.
Risolvere un triangolo rettangolo ABC con angolo retto in A dati l'ipotenusa a=20 e γ=20°
L'angolo β si determina facilmente con una differenza ovvero: β=90°-20°=70°.
Il cateto b si determina con la seguente formula: b=a*sinβ ovvero sostituendo b=20*sin(70°)=18,794, Il cateto c si determina con la seguente formula: c=a*sinγ ovvero sostituendo c=20*sin(20°)=6,84. A questo punto riserviamo il teorema di Pitagora per l'eventuale verifica.
Risolvere un triangolo rettangolo ABC con angolo retto in A dati l'angolo β=16°15'37'' ed il cateto c=12
L'angolo γ si determina facilmente con una differenza ovvero: γ=90°-16°15'37''=73°44'23''.
L'ipotenusa si determina con la seguente formula: a=c/cosβ ovvero sostituendo a=12/cos(16°15'37'')=12,5. Il cateto b si determina con la seguente formula: b=c*tanβ ovvero sostituendo b=12*tan(16°15'37'')=3,5. A questo punto riserviamo il teorema di Pitagora per l'eventuale verifica. Come si può notare si sono usate le formule che sfruttano i dati del problema, quindi non dati calcolati in precedenza che potrebbero essere errati o contenere errori dovuti al troncamento delle cifre dopo la virgola.
Risolvere un triangolo rettangolo ABC con angolo retto in A dati l'angolo β=65° ed il cateto b=7,25
L'angolo γ si determina facilmente con una differenza ovvero: γ=90°-65°=25°.
L'ipotenusa si determina con la seguente formula: a=b/sinβ ovvero sostituendo a=7,25/sin(65°)=8. Il cateto c si determina con la seguente formula: c=b/tanβ ovvero sostituendo c=7,25/tan(65°)=3,38. A questo punto riserviamo il teorema di Pitagora per l'eventuale verifica. Come si può notare si sono usate le formule che sfruttano i dati del problema, quindi non dati calcolati in precedenza che potrebbero essere errati o contenere errori dovuti al troncamento delle cifre dopo la virgola.
Risolvere un triangolo rettangolo ABC con angolo retto in A dati l'ipotenusa a=17 e il cateto b=15
Si potrebbe determinare l'ipotenusa applicando il teorema di Pitagora, si consiglia di applicare le formule della trigonometria per far pratica sulle stesse, riservando il teorema di Pitagora per l'eventuale verifica.
Sfruttiamo la seguente formula: sinβ=b/a, da cui ricaviamo l'angolo β: β=sin-1(b/a),
ovvero sostituendo:
β=sin-1(15/17)=61°55'39''. L'angolo γ si può calcolare nel seguente modo:
γ=cos-1(b/a) ovvero γ=cos-1(15/17)=28°4'21''. Se i calcoli sono esatti
β+γ=90°. Il cateto c si può trovare con la seguente formula: c=a*sinγ, sostituendo c=17*sin(28°4'21'')=8.
Il teorema di Pitagora sarà utile per la verifica.
esercizi
esercizi
β=10°; a=5
[b=0,868; c=4,924; γ=80°]b=15; c=8
[a=17; β=61°55'39''; γ=28°04'21'']b=8; c=16
[a=17,89; β=26°33'54''; γ=63°26'06'']a=20; β=28°53'22'';
[b=9,66; c=17,51; γ=61°06'38'']b=32,25; β=37°42'53''
[a=52,72; c=41,70; γ=52°17'07'']a=22; β=35°25'32''
[b=12,75; c=17,93; γ=54°34'28'']b=17,25; β=28°32'15'';
[a=36,11; c=31,72; γ=61°27'45'']a=14,93; b=10,32
[c=10,79; β=43°43'38''; γ=46°16'22'']a=22,84; β=43°26'12'';
[b=15,70; c=16,59; γ=46°33'48'']b=8,7; a=17,3;
[β=30°11'29''; c=14,95; γ=59°48'30'']β=10°40'20''; a=20;
[γ=79°19'40''; c=19,65; b=3,7]c=42; γ=53°36'18'';
[β=36°23'42''; a=52,17; b=11,86]c=40; γ=50°32'52'';
[β=39°27'07''; a=51,8; b=32,91]
Risolvere un triangolo rettangolo ABC con angolo retto in A dati i seguenti elementi:
Risoluzione triangoli qualunque
Negli esercizi che seguono si faccia sempre riferimento ad un triangolo di questo tipo:
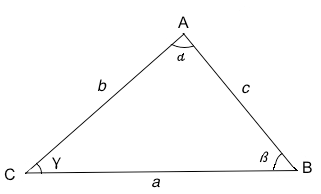
dati:
a=10 b=8 c=12
Si usa il teorema del coseno per calcolare α ovvero α=cos-1(b2+c2-a2/2bc). Se b2+c2-a2/2bc non avesse un valore compreso tra -1 e 1 il problema sarebbe impossibile, infatti la funzione arcocoseno ha per dominio l'intervallo [-1,1], in altre parole si può creare un triangolo solo se la somma di due qualunque lati sia maggiore del terzo lato. Sostituendo: α=cos-1(82+122-102/2*8*12)=55°46'41", analogamente γ=82°49'14" e β=41°24'30''. A questo punto si verifichi che la somma dei tre angoli sia 180°.
Esercizio 1
dati:
a=12, c=8, γ=40°
Applichiamo il teorema del seno.
sinα=a*sinγ/c da cui: α=sin-1(a*sinγ/c), ovvero sostituendo: α=sin-1(12*sin(40°)/8)=74°37'7". A questo punto bisogna tener conto che , siccome la funzione arcoseno ha per insieme immagine angoli non più grandi di 90°, oltre a l'angolo trovato bisogna prendere in considerazione l'angolo 180°-α ovvero α2=180°-74°37'7"=105°22'53". L'angolo trovato con il primo passaggio pari a 74°37'7" lo chiamiamo quindi α1. A questo punto è chiaro che ci sono due soluzioni, ovvero due triangoli che soddisfano alle condizioni iniziali. Se chiediamo quindi ad un disegnatore dotato di matita, righelli, compasso e goniometro, di tracciare il triangolo, con i dati del probema, prima traccerà il lato a, quindi con il goniometro l'angolo γ traccerà poi una circonferenza con centro in B e con apertura del compasso pari alla misura del lato c, si accorgerà a questo punto che la circonferenza intersecherà il lato b in due punti. Per trovare quini β1 si esegue una differenza ovvero β1=180°-(γ+α1) ovvero sostituendo β1=180°-(40°+74°37'7")=65°22'53", analogamente β2=180°-(40°+105°22'53")=34°37'7". A questo punto calcoliamo b1 e b2 con il teorema del seno: b1=c*sinβ1/sinγ sostituendo b1=8*sin65°22'53"/sin40°=11,31 analogamente b2=c*sinβ2/sinγ sostituendo b2=8*sin34°37'7"/sin40°=7,07. Infine controliamo sempre che ad angolo maggiore sia opposto lato maggiore.
Esercizio 2
dati:
a=34, c=30, γ=61°55'39"
Applichiamo il teorema del seno.
sinα=a*sinγ/c da cui: α=sin-1(a*sinγ/c), ovvero sostituendo: α=sin-1(34*sin(61°55'39'')/30). Il valore in parentesi (34*sin(61°55'39")/30) risulta essere uguale 1 per cui α=90°. La soluzione è quindi unica. L'angolo β lo ricaviamo con una differenza: β=180°-(61°55'39''+90°)=28°4'21". Il lato b lo troviamo quindi con la seguente formula: b=a*cosγ sostituendo: b=34*cos(61°55'39'')=16. Se chiediamo quindi ad un disegnatore dotato di matita, righelli, compasso e goniometro, di tracciare il triangolo, con i dati del probema, prima traccerà il lato a, quindi con il goniometro l'angolo γ traccerà poi una circonferenza con centro in B e con apertura del compasso pari alla misura del lato c, si accorgerà a questo punto che la circonferenza è tangente il lato b.
Esercizio 3
dati:
a=11, c=3, γ=45°
Applichiamo il teorema del seno.
sinα=a*sinγ/c da cui: α=sin-1(a*sinγ/c), ovvero sostituendo: α=sin-1(11*sin45°/3). Il valore in parentesi (11*sin45°/3) risulta essere maggiore di 1 per cui il problema è impossibile poichè il dominio della funzione sin-1 è l'intervallo [-1;1]. Se chiediamo quindi ad un disegnatore dotato di matita, righelli, compasso e goniometro, di tracciare il triangolo, con i dati del probema, prima traccerà il lato a, quindi con il goniometro l'angolo γ traccerà poi una circonferenza con centro in B e con apertura del compasso pari alla misura del lato c, si accorgerà a questo punto che la circonferenza non intersecherà il lato b.
dati:
b=36,8 c=30 α=78°58'12"
Teniamo presente che la soluzione esiste comunque siano i dati ed è unica. Si usa necessariamente il teorema del coseno per ricavare il lato a ovvero: a=√b2+c2-2bc*cosα e sostituendo a=√ 36,82+302-2*36,8*30*cos(78°58'12'') =42,8
A questo punto per determinare la misura dei degli altri due angoli si può utilizzare o il teorema dei seni o il teorema del coseno. Per il teorema del coseno β=cos-1(a2+c2-b2/2ac). Per il teorema del seno β=sin-1(b*sinα/a). Nell'applicare il teorema del seno si deve tener conto che la funzione arcoseno non apprezza angoli maggiori di 90° per cui bisognerebbe considerare oltre all'angolo dato anche l'angolo 180°-α e determinare quale dei due angoli può essere preso come soluzione valutando che ad angolo maggiore sta opposto lato maggiore. Per evitare ciò si può utilizzare il teorema del coseno β=cos-1(a2+c2-b2/2ac) sostituendo: β=cos-1(42,82+302-36,82/2*42,8*30)=57°33'14" analogamente γ=cos-1(42,82+36,82-302/2*42,8*36,8)=43°28'34". Come verifica si può controllare che la somma dei tre angoli sia 180°.
dati:
dati a=20 e gli angoli β=60° γ=50°.
Se chiediamo ad un disegnatore dotato di matita, righelli, compasso e goniometro, di tracciare il triangolo, con i dati del probema, prima traccerà il lato a, quindi con il goniometro i due angoli β e γ adiacenti ad a stesso, il punto d'incontro dei lati degli angoli β e γ sarà proprio il vertice A. Ci si accorge che se β+γ<180°, la soluzione esiste ed è unica. Per risolvere il problema, innanzitutto si determina l'angolo α con una differenza ovvero: α=180°-(β+γ), sostituendo α=180°-(60°+50°)=70°. Per determinare b e c si usa il teorema dei seni ovvero: b=a*sinβ/sinα, c=a*sinγ/sinα, sostituendo: b=20*sin60°/sin70°=18,42 c=20*sin50/sin70°=16,3.
esercizi
esercizi
Risolvere un triangolo ABC dati i seguenti elementi
a=25 b=15 c=20
[α=90°; β=36°52'12"; γ=53°7'48"]a=2 b=5 c=6
[α=18°11'42" β=51°19'04" γ=110°29'14"]a=7 b=8 c=16
[impossibile]a=15 β=32°23'15" γ=53°04'12"
[α=94°32'33" b=8,06; c=12,03]a=5 b=3 β=36°52'11"
[α=90° γ=53°07'48" c=4]a=15 α=84°22'22" β=35°23'32"
[b=8,73 c=13,08 γ=60°14'06"]a=25 b=14 β=73°12'32"
[impossibile]a=20 b=11 β=28°30'30"
[α1=60°12'12" γ1=91°17'18" c1=23,04; α2=119°47'48" γ2=31°41'42" c2=12,11]b=15,23 c=12,24 β=101°22'33"
[a=6,96 α=26°38'08" γ=51°59'19"]a=532 b=486 β=73°22'22"
[impossibile]a=532 b=486 β=43°32'11"
[α1=48°56'21" γ1=87°31'28" c1=704,90; α2=131°03'39" γ2=5°24'10" c2=66,43]a=85 b=101 β=97°15'31"
[α=56°35'57" γ=26°08'32" c=44,86]a=24 b=17 γ=97°14'47"
[α=49°55'47" β=32°49'26" c=31,11]a=10 b=12,21 γ=38°22'43"
[α=54°51'18" β=86°45'59" c=7,59]a=22,84 c=19,23 γ=5°23'12"
[α1=6°24'06" β1=168°12'42" b1=41,85; α2=173°35'54" β2=1°00'54" b2=3,63]a=32 b=47 c=19
[α=30°02'46'' β=132°39'31" γ=17°17'41"]a=18,72 b=8,33 γ=41°24'
[α=114°46' β=23°50' c=13,63]a=25,37 b=59,31 γ=23°43'51"
[α=15°47'54" β=140°28'15" c=37,50]a=23 c=15 γ=37°32'43"
[α1=69°07'50" β1=73°19'27" b1=23,58; α2=110°52'10" β2=31°35'07" b2=12,89]a=68 β=34°51'07" γ=52°34'12"
[α=92°34'41" b=38,9 c=54,05]a=314 β=10°10'09" γ=51°37'13"
[α=118°12'38" b=62,91 c=279,32]