Combinazioni
Con la tabella possiamo, dato un insieme di cinque elementi, determinare quanti sono i suoi sottoinsiemi di due elementi.
Per esempio se numeriamo questi oggetti dal numero uno al cinque, ogni riga della tabella rappresenta un diverso sottoinsieme.
Possiamo concludere che 10 esprime il numero dei sottoinsiemi di 2 elementi che si possono costituire in un insieme di 5 elementi.
Sarebbe lo stesso se volessimo determinare il numero dei sottoinsiemi di tre elementi, in tal caso basterebbe conteggiare il numero dei sottoinsiemi complementari ai precedenti.
Il numero così trovato, viene detto numero delle combinazioni di n elementi di classe k e si indica con C(n,k).
Il ragionamento fatto ci mostra che è: (5,3) = (5,2), questo perchè in un insieme di 5 elementi sceglierne 2, equivale a scartarne 3.
| 1 | 2 | 3 | 4 | 5 |
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X |
Triangolo di Tartaglia
In opere cinesi del 1100 a.c. circa si fa riferimento a sistemi di tabulazione per coefficienti dello sviluppo della potenza di un binomio: è verosimile che quella tabella di numeri, nota in occidente con il nome di "triangolo di Pascal" o "triangolo di Tartaglia" abbia avuto origini in Cina intorno a tale data.
I numeri del triangolo rappresentano le "combinazioni" ovvero il numero di sottoinsiemi di k elementi in un insieme di n elementi.
| 1 | ||||||||||||||||||
| 1 | 1 | |||||||||||||||||
| 1 | 2 | 1 | ||||||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||||||||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
Proprietà del triangolo
Sono due le proprietà che presenta questo famoso triangolo.
La prima è data dalla simmetria del triangolo che può essere riassunta dalla seguente formula:
C(n,k)=C(n,n-k)
La seconda proprietà è che, ogni numero di una certa riga è dato dalla somma dei due numeri che si trovano nella precedente riga, il primo nella stessa diagonale, il secondo nella diagonale sucessiva. Questa caratteristica si riassume nella seguente formula:
C(n,k)=C(n-1,k)+C(n-1,k-1)
Sviluppo del binomio
Il triangolo di Tartaglia consente di individuare i coefficienti dello sviluppo di un binomio (a+b) elevato alla n-esima potenza. I coefficienti dei singoli termini sono dati dai numeri della (n+1)-esima riga del triangolo. Proponiamoci di sviluppare l'espressione (x+y)2, dove n è un intero positivo (potenza n-sima del binomio). Sappiamo che si ha (x+y)2 =x2 + 2xy + y2 e con un semplice calcolo si trova: (x+y)3 =x3+3x2y+3xy2+ y3
I monomi che si ottengono dallo sviluppo di (x+y)2 e di (x+y)3 li possiamo rappresentare mediante un grafo simile a quello della figura
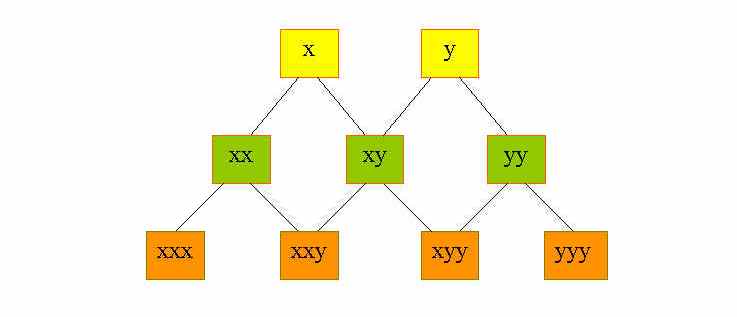
ad ogni cammino sul grafo corrisponde un monomio, per esempio il percorso sinistra sinistra destra partendo da sopra corrisponde al monomio xxy. Il grafo sembra analogo a quello che rappresenta il lancio della moneta. Per la proprietà commutativa della moltiplicazione, due monomi contenenti lo stesso numero di volte le x, e le y, diventano simili. Ad esempio, i due monomi xyx e xxy sono simili. Il problema è allora quello di contare i monomi che diventano simili traloro. Conviene quindi modificare il grafo facendo confluire in uno stesso vertice i cammini che corrispondono a monomi simili. Il nostro problema si riduce a quello di contare il numero dei cammini che arrivano ad un dato vertice in un grafo come quello della figura. Teniamo presente che, quando conteggiamo dei percorsi, intendiamo sempre che si parte da sopra e si percorre la via più breve per arrivare ad un certo incrocio.
Possiamo concludere così: lo sviluppo di (x+y)n è costituito dalla somma di tutti i monomi del tipo xn-k yk moltiplicati per i coefficienti (n,k) che sono i numeri del triangolo di Tartaglia-Pascal.
Ricordiamo che è: (n,n) = (n,0) = 1 (n,1) = (n,n-1) = n
Indichiamo con n il numero delle righe,
tenendo presente che la prima riga, quella con il solo numero 1 è la riga zero. Indichiamo con k il numero delle diagonali,
tenendo presente che la prima diagonale, quella formata da tutti numeri 1, è la diagonale zero.
Sviluppando (x+y)5 otteniamo x5+5x4y+10x3y2+10x2y3+5xy4+y5.
Esempi di combinazioni
Gli esempi che seguono riguardano l'arte di saper contare e trattano eventi anche estremamente diversi tra di loro. Il conteggio del numero di un certo tipo di monomi nello sviluppo del binomio, però risulta perfettamente analogo a quello di contare i percorsi della pallina che scende in una serie di canaletti. La stessa casa la possiamo dire per lancio monete, per il conteggio dei percorsi in una città a pianta romana, per il conteggio degli anagrammi di parole formate da due lettere. Si tratta in ogni caso dei numeri del triangolo di Tartaglia, in altre parole del conteggio dei sottoinsiemi di un insieme.
Lancio della moneta
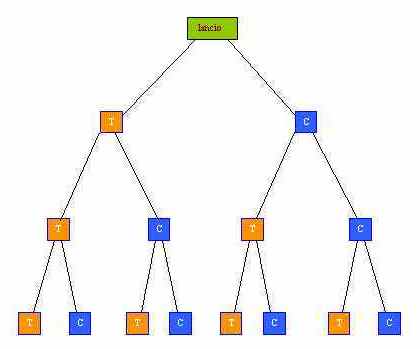
| T | T | T |
| T | T | C |
| T | C | T |
| C | T | T |
| C | C | T |
| C | T | C |
| T | C | C |
| C | C | C |
Lanciamo una, due, tre volte una moneta. Gli eventi possibili sono rappresentati dalla tabella o dai vari cammini di un grafo ad albero come in figura. Essi possono essere elencati così, indicando con T "testa" e con C "croce": In tutto sono 8. Gli eventi che si possono verificare nel lancio di una moneta n volte sono 2n: infatti, per n = 1 sono 2: T, C, e ad ogni lancio il numero degli eventi precedentemente elencati è raddoppiato. Per esempio se lanciamo otto volte una moneta ci saranno 256 casi possibili, se poi ci chiediamo quante volte può verificarsi l'evento: 2 teste, 6 croci, dovremo ricercare il secondo elemento, contando a partire dallo zero, della ottava riga del triangolo che è 28, oppure il sesto elemento della stessa riga, che è comunque sempre 28. In generale, consideriamo ora il caso di n lanci: ci chiediamo in quanti casi T si presenta k volte (essendo, naturalmente, 0≤k≤n) e, ovviamente, C si presenta n-k volte. A questo scopo, conviene fare ricorso ad un tipo di grafo, più espressivo, che non è più "ad albero". In questo grafo, i cammini diversi che arrivano ad uno stesso vertice contengono uno stesso numero di T e di C, in ordine diverso. Ad esempio per n=3, il vertice che corrisponde a "2 volte T ed una volta C", viene raggiunto attraverso 3 cammini.
Percorsi in una città a pianta romana ... per la via più breve
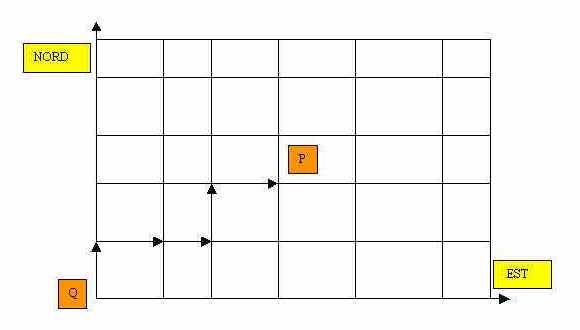
Risolviamo un piccolo problema: la pianta di una città sia come nella figura; le linee orizzontali e verticali rappresentano le vie. Un turista parte dal punto Q; ad ogni incrocio egli va, a caso, verso est oppure verso nord (lanciando una moneta). La situazione è solo in apparenza diversa da quella considerata nel lancio di una moneta; in realtà, basta intendere che T significhi tratto verso e C tratto verso nord.
I numeri di Pascal ci dicono in questo caso in quanti modi diversi, per la strada più breve, posso giungere per esempio all'incrocio P. Possiamo osservare, in linea generale, che uno dei vantaggi più forti che ci dà una formazione matematica, è quello di riconoscere che, in molti casi, situazioni all'apparenza diverse hanno una stessa struttura astratta e possono essere chiarite con lo stesso ragionamento. Nel nostro caso, dunque, il numero delle strade che arrivano a P è dato da:(5,3)=(5,2)=10
Una pallina che scende in una serie di canaletti
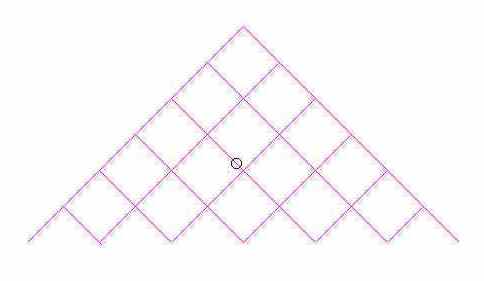
Si pensi che le linee in figura siano canalini nei quali possa correre una pallina la quale, situata inizialmente in cima, cada. Si supponga che, ad ogni bivio non vi siano ragioni per ritenere che la pallina proceda verso destra, piuttosto che verso sinistra.
Si vuole determinare la probabilità che, ad un certo livello, la pallina venga a trovarsi in un certo vertice A(k).
Ragionando come nella determinazione del numero di strade che portano ad un certo incrocio, possiamo contare il numero dei casi favorevoli, quindi C(n,k), mentre i casi possibili si otterranno dalla somma di tutti i numeri del livello n-imo in altre parole 2n.
Volendo fare gli anagrammi, anche privi di significato, della parola mamma compiliamo una tabella come quella in figura.
La somiglianza con una tabella come quella che individua i sottoinsiemi di due elementi in un insieme di cinque elementi è notevole: basta sostituire alle “A” le “X” e non mettere niente al posto della “M” che le tabelle sono uguali.
In altre parole in un insieme di cinque caselle, bisogna scegliere i sottoinsiemi di due caselle nei quali inserire la lettera A, nelle altre caselle poi, inseriremmo la lettera M.
Quindi il numero di anagrammi della parola mamma sarà uguale al numero di Pascal che si trova nella quinta riga e seconda diagonale del triangolo ovvero corrisponde al numero di colonne della tabella in figura cioè 10.
Il ragionamento ci permette quindi, di determinare quanti sono gli anagrammi di quelle parole come nonno, Anna, non, papà, composte da due sole lettere.
| A | A | M | M | M |
| A | M | A | M | M |
| A | M | M | A | M |
| A | M | M | M | A |
| M | A | A | M | M |
| M | A | M | A | M |
| M | A | M | M | A |
| M | M | A | A | M |
| M | M | A | M | A |
| M | M | M | A | A |
Conteggio dei sottoinsiemi
Nella figura di sotto si associa ad un determinato percorso un sottoinsieme, "vai a destra" potrebbe voler dire che l'elemento di quel livello appartiene al sottoinsieme, "vai a sinistra" invece, che non appartiene al sottoinsieme. Per esempio consideriamo come insieme universo, {a, b, c, d, e, f} il percorso della figura di destra corrisponde al sottoinsieme {b, c, f}.
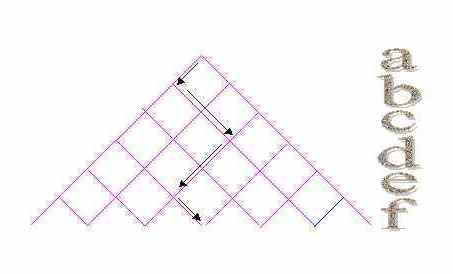
Il numero C(n,k) è quindi il numero che si trova all'incrocio della n-esima riga e k-esima diagonale del triangolo di Tartaglia. C(n,k) è detto numero delle combinazioni di n elementi di classe k. Si noti che il triangolo che serve a determinare i coefficienti dello sviluppo del binomio qui, lo stesso triangolo, serve a conteggiare il numero di sottoinsiemi di un insieme.
Come determinare la formula delle combinazioni
Cerchiamo di determinare C(n,k), ovvero un numero del triangolo di Tartaglia Pascal attraverso una formula,
senza dover compilare tutte le righe precedenti alla n-esima. Ci aiutiamo risolvendo un semplice problema.
Il problema è il seguente: in quanti modi possiamo disporre k studenti in n banchi, pensando che ogni
studente può occupare un unico banco e che il numero degli studenti sia minore al numero dei banchi.
Risolviamo il problema in due modi diversi.
primo ragionamento: possiamo pensare che il primo studente, che sceglie il banco, può farlo in
n modi, il secondo trovando un banco già occupato può farlo in n-1 modi,
il terzo trovando due banchi già occupati può farlo in n-2 modi e così via, fino a che, l'ultimo,
cioè il k-eimo studente, trovando n-(k-1) banchi già occupati, può
scegliere tra gli n-k+1 banchi rimasti. In definitiva si tratta di disposizioni semplici ed il numero
che si ottiene è: n(n-1)(n-2) ... (n-k+1)
secondo ragionamento: si può anche partire pensando a come sarà la disposizione finale degli
studenti.
Quando tutti avranno scelto il banco, ci saranno k banchi occupati da k studenti, quindi innanzitutto,
bisogna conteggiare in quanti modi diversi si possono scegliere i k banchi che saranno occupati dai k
studenti. In altre parole bisogna conteggiare quanti sono i sottoinsiemi di k banchi in un insieme di
n banchi. Ovviamente il numero è quello che si trova all'incrocio della n-esima riga con la k-esima
diagonale del triangolo di Tartaglia Pascal cioè le combinazioni C(n,k). Una volta scelti i k banchi
che saranno occupati, bisogna pensare in quanti modi diversi i k studenti possono disporsi nei k banchi.
Si tratta di permutazioni per cui il numero è: k!, quindi con questo ragionamento otteniamo: C(n,k)k!
Anche se il secondo ragionamento è un pò più complicato del primo, risulta comunque valido, e deve
produrre lo stesso risultato, per cui si
potrà scrivere: C(n,k)k!=n(n-1)(n-2) ... (n-k+1).
A questo punto ci si comporta come se quella
scritta fosse un'equazione di primo grado avente per incognita C(n,k). Risolta l'equazione si trova che:
C(n,k) = n(n-1)(n-2) ... (n-k+1)/k!