Indici di dispersione
Gli indici si distinguono in:
1. Indici di dispersione assoluta, che sono espressi nella stessa unità di misura del fenomeno osservato.
2. Indici di dispersione relativa, che prescindono dall’unità di misura e possono presentarsi sotto forma di percentuale.
Indici assoluti di dispersione
Campo di variazione
Se i dati sperimentali della distribuzione sono di carattere quantitativo, le diverse modalità rilevate possono essere ordinate dalla più piccola alla più grande: x1, x2, x3...xn
Definizione: il campo di variazione è la differenza tra il valore massimo ed il valore minimo C.V.=xn-x1.
Scarto semplice medio
Definizione: lo scarto medio semplice di una serie di valori sperimentali x1, x2,...xn è dato dalla sommatoria delle differenze in valore assoluto tra i dati sperimentali xi e la media aritmetica M dei valori diviso il numero dei dati n.
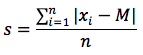
Scarto quadratico medio
Definizione: lo scarto quadratico medio di una serie di valori sperimentali x1, x2, ... xn è dato dalla radice quadrata della media aritmetica dei quadrati degli scarti dalla loro media aritmetica.
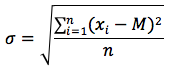
Varianza
Definizione: la varianza è la media degli scarti quadratici medi elevati al quadrato.
La varianza, si indica con σ2 poichè corrisponde al quadrato dello scarto quadratico medio.
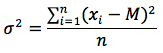
La distribuzione Gaussiana e lo scarto quadratico medio

In figura la banconota più diffusa in Germania, prima dell'avvento dell'euro, la banconota da 10 marchi tedesca che riporta l'immagine del Gauss con sullo sfondo la formula ed il grafico della curva gaussiana.
La distribuzione Gaussiana è la più importante distribuzione statistica, si chiama anche distribuzione normale in quanto molti fenomeni complessi, ma collegati a situazioni reali possono essere descritti da una curva di questo tipo. La particolarità di questa curva è che le frequenze più elevate si hanno nei valori centrali e con frequenze progressivamente minori verso gli estremi della variabile a disporsi secondo curva detta a campana. E' chiamata anche curva degli errori accidentali, in quanto, nella misurazione ripetute di una certa grandezza fisica si possono commettere degli errori, ma le varie misure tendono a concentrarsi attorno a un singolo valor medio. La distribuzione Gaussiana è caratterizzata dalla seguente funzione di densità di probabilità, cui spesso si fa riferimento con la dizione di curva di Gauss o gaussiana:
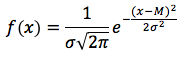
dove con M si è indicata la media aritmetica, con σ lo scarto quadratico medio, e rappresenta il numero di Nepero, x rappresenta i valori presi in esame. Il calcolo dello scarto quadratico medio è molto importante nelle distribuzioni gaussiane. In una distribuzione Gaussiana infatti, lo scarto quadratico medio σ, permetta di conoscere l'intervallo, centrato sulla media, attorno a cui si concentra un determinato numero di dati.
| intervallo | valori in percentuale |
|
| inf | sup | |
| x m - σ | x m + σ | 68,27 |
| x m - 2σ | x m + 2σ | 95,45 |
| x m - 3σ | x m + 3σ | 99,73 |
Si può dimostrare che se x m è la media aritmetica della distribuzione, negli intervalli:
[xm - σ , xm + σ] cade il 68,27% dei dati.
[x m-2σ , x m+2σ] cade il 95,45% dei dati.
[x m-3σ, x m+3σ] cade il 99,73% dei dati.
Nella tabella a sinistra un riepilogo della situazione.
Differenza media semplice
| 2 | 4 | 6 | 7 | 8 | 10 | ||
| 2 | 0 | 2 | 4 | 5 | 6 | 8 | 25 |
| 4 | 0 | 2 | 3 | 4 | 6 | 15 | |
| 6 | 0 | 1 | 2 | 4 | 7 | ||
| 7 | 0 | 1 | 3 | 4 | |||
| 8 | 0 | 2 | 2 | ||||
| 10 | 0 | 0 | |||||
| semitotale | 54 | ||||||
| totale | 108 | ||||||
Gli indici di variabilità come campo di variazione, scarto semplice medio, scarto quadratico medio, varianza, si ottengono determinando gli scarti tra le modalità del carattere e la sua media.
La differenza media semplice, invece, si ottiene sommando le differenze in valore assoluto delle modalità del carattere prese a due a due. In tabella, per esempio, si sono calcolate le differenze medie in valore assoluto di sei numeri: 2, 4, 6, 7, 8, 10.
Sono stati ordinati in ordine crescente e in ogni cella è stata calcolata la differenza in valore assoluto tra il numero della stessa colonna e nella prima riga ed il numero della stessa riga e prima colonna.
La parte della tabella che stà al di sotto della diagonale non è stata compilata per semplificare il calcolo del totale in quanto la tabella è simmestrica rispetto alla diagonale stessa.
Nell'ultima riga infine sono state calcolate le somme di ogni riga e, sommando tutti questi valori, si è ottenuto 54 che rappresenta la semisomma di tutti i valori.
La somma è quindi il doppio appunto perchè metà della tabella non è stata completata,ovvero 108.
Dividendo questo numero per 30 che rappresenta il numero dei valori, presenti in tabella, diversi da zero, otteniamo la differenza media che è 3,6. Più in genere, se il numero dei valori è n, il numero delle celle presenti in tabella sarà n2 però in una diagonale ci saranno n valori uguali a zero. I valori diversi da zero saranno quindi n2-n=n(n-1). La differenza media Δ, sarà calcolata sui n(n-1) dati diversi da zero.
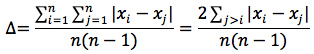
Indici relativi di dispersione
Il coefficiente di variazione
Definizione: il coefficiente di variazione, di un dato campione, è il rapporto tra lo scarto quadratico medio σ e il valore assoluto della sua media aritmetica.
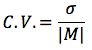
E' un indice di dispersione che permette di confrontare misure di fenomeni riferite a unità di misura differenti, in quanto si tratta di un numero puro. Si può esprimere anche in termini di percentuale moltiplicando il valore ottenuto per cento. Si noti che ha senso calcolarlo solo per campioni aventi la media aritmetica non nulla.
Esempio 1
| media | σ | C.V. | |
| Milano | 10,50 | 3,15 | 0,3 |
| Roma | 9,20 | 2,98 | 0,32 |
Supponiamo di voler confrontare i prezzi di un bene di consumo in due città, Roma e Milano. Dopo aver raccolto i dati supponiamo di aver ottenendo i risultati in tabella. Confrontando gli scarti quadratici, saremo portati a dire che i prezzi a Milano abbiano una variabilità maggiore. Però, dobbiamo calcolare la variabilità rispetto al valore medio ovvero va confrontato il coefficiente di variazione, dal quale si deduce che a Roma i prezzi hanno una variabilità più elevata che a Milano.
Esempio 2
| media | σ | C.V. | |
| stipendi | €1250 | €320 | 0,25 |
| età | 43 | 15 | 0,34 |
Se l'uso del coefficiente di variazione è utile per confrontare fenomeni della stessa natura, a maggior ragione è ancora più importante quando si confrontano fenomeni che hanno caratteristiche ed unità di misura diverse. In una ditta si sono rilevati gli stipendi e l'età degli impiegati. Dopo aver calcolato media e scarto quadratico medio si sono ottenuti i valori dei coefficienti di variazine riportati in tabella. Si sono così confrontati dati con caratteristiche estremamente diverse.
La concentrazione
La concentrazione è un aspetto della variabilità di un fenomeno. Per esemplificare, tra gli abitanti di un paese dell'europa occidentale non ci sono grandi disparità di ricchezza perchè non ci sono grandi differenze di reddito, in Russia, invece, la ricchezza è concentrata in poche persone. L'analisi della concentrazione serve ad indicare quanto un fenomeno è uniformemente distribuito oppure è concentrato in poche unità.
Uno strumento che permette di valutare il grado di concentrazione è la curva di Lorenz chiamata anche spezzata di concentrazione. Questa curva è una funzione, il cui grafico è ottenuto unendo con dei segmenti i punti che hanno per ascissa e ordinata rispettivamente le frequenze relative cumulate e le intensità relative cumulate del fenomeno. Viene definita area di concentrazione la regione di piano che è delimitata dalla bisettrice y=x, e dalla spezzata di concentrazione. Maggiore è quest'area, maggiore è la concentrazione. Se le frequenze cumulate fossero uguali alle intensità cumulate si avrebbe una equidistribuzione del reddito, ovvero tutti avrebbero lo stesso reddito e quindi stessa ricchezza. In tal caso, la spezzata di concentrazione corrisponderebbe ad un tratto della retta y=x. Si osservi che tanto più la spezzata si avvicina alla retta di equidistribuzione, ovvero tanto minore è l'area di concentrazione, più la ricchezza è distribuita equamente. Il caso estremo si verifica nel caso in cui nessuno possiede ricchezza, tranne gli appartenenti all'ultima classe. In questo caso la spezzata di concentrazione è costituita dal triangolo rettangolo isoscele, che ha per ipotenusa un tratto della retta bisettrice il primo e terzo quadrante e che ha un'area pari a 0,5. Questo triangolo costituisce l'area di massima concentrazione. Il rapporto di concentrazione è dato dal rapporto tra l'area di concentrazione e l'area di massima concentazione. Attraverso un esempio vediamo come si possa calcolare questo indice che si può anche esprimere in termini di percentuale.
EsempioIn una ditta lavorano 30 persone, inquadrate in sei classi stipendiali, ciò significa che gli stipendi non sono tutti uguali, quindi, come si può notare nella tabella, la somma totale a disposizione dei 30 lavoratori, non è egualmente distribuita. Innanzitutto valutiamo a quanto ammontano le somme di danaro a disposizione dei lavoratori di ogni classe stipendiale, moltiplicando il valore centrale della classe per la frequenza, ossia per il numero dei lavoratori della classe stipendiale. In presenza di una distribuzione di frequenza in classi, nel calcolo della media è necessario individuare, per ogni classe un valore rappresentativo della stessa. Si introduce il concetto di valore centrale della classe. Esso è ottenuto come semi-somma degli estremi di ogni classe. La media è calcolata come media ponderata dei valori centrali per le rispettive frequenze delle classi. Il valore ottenuto rappresenta l'intensità della classe. La frequenza cumulata si calcola sommando ai valori della classe, quelli delle classi precedenti. L'intensità cumulata si calcola sommando ai valori della classe, quelli delle classi precedenti. Addizionando i valori di tutte le classi otteniamo 33150 che è l'intensità globale del fenomeno.
Analizzando le colonne della frequenza cumulata e della intensità cumulata, notiamo che:
2 lavoratori hanno a disposizione 1300 euro dei 33150 euro complessivi,
9 lavoratori hanno a disposizione 7600 euro dei 33150 euro complessivi,
19 lavoratori hanno a disposizione 18600 euro dei 33150 euro complessivi,
27 lavoratori hanno a disposizione 28600 euro dei 33150 euro complessivi,
29 lavoratori hanno a disposizione 31400 euro dei 33150 euro complessivi, in termini percentuali quindi,
il 6,6% dei lavoratori riceve il 3,9% dell'ammontare complessivo,
il 30% dei lavoratori riceve il 22,9% dell'ammontare complessivo,
il 63,3% dei lavoratori riceve il 56% dell'ammontare complessivo,
il 90% dei lavoratori riceve il 86,2% dell'ammontare complessivo,
il 96,6% dei lavoratori riceve il 94,7% dell'ammontare complessivo.
| stipendio | valore centrale | frequenza | intensità | frequenza cumumulata | intensità cumulata | frequenza relativa cumulata | intensità relativa cumulata | calcolo area trapezi (B+b)h/2 | area trapezi | ||
| min | max | ||||||||||
| 500 | 800 | 650 | 2 | 1300 | 2 | 1300 | 0,066 | 0,0392 | (0,0392+0)(0,066)/2 | 0,0013 | |
| 800 | 1000 | 900 | 7 | 6300 | 9 | 7600 | 0,3 | 0,2292 | (0,2292+0,0392)(0,3-0,066)/2 | 0,0313 | |
| 1000 | 1200 | 1100 | 10 | 11000 | 19 | 18600 | 0,633 | 0,560 | (0,560+0,2292)(0,633-0,3)/2 | 0,1317 | |
| 1200 | 1300 | 1250 | 8 | 10000 | 27 | 28600 | 0,9 | 0,8627 | (0,8627+0,560)(0,9-0,633)/2 | 0,1898 | |
| 1300 | 1500 | 1400 | 2 | 2800 | 29 | 31400 | 0,966 | 0,9472 | (0,9472+0,8627)(0,966-0,9)/2 | 0,0603 | |
| 1500 | 2000 | 1750 | 1 | 1750 | 30 | 33150 | 1 | 1 | (1+0,9472)(1-0,966)/2 | 0,0324 | |
| somma aree trapezi | 0,4469 | ||||||||||
Inseriamo in un diagramma cartesiano i punti che hanno per ascissa le frequenze relative cumulate e per ordinata le rispettive intensità relative cumulate. Questi punti, che sono contenuti in un quadrato di lato unitario, costituiscono gli estremi di segmenti che vanno a costituire la spezzata di concentrazione.
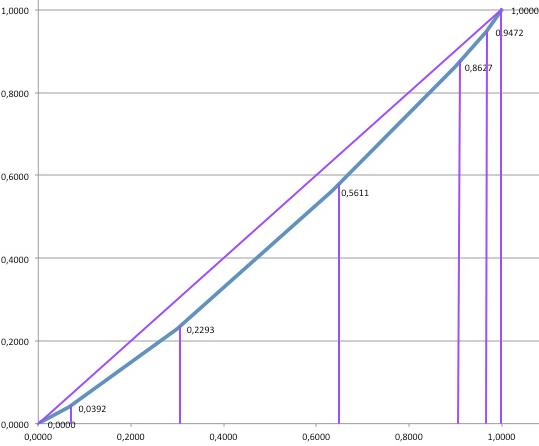
Ora si deve determinare l'area di concentrazione che è compresa tra la retta di equidistribuzione e la spezzata di concentrazione. Quest'area è data dalla differenza tra 0,5 che è l'area del triangolo rettangolo isoscele che ha per ipotenusa la retta di equidistribuzione e l'area che stà al di sotto della retta di concentrazione. Quest'ultima area si ottiene sommando le aree dei trapezi rettangoli, in nero, che stanno al di sotto della spezzata di concentrazione e che hanno per altezza la differenza tra le frequenze relative cumulate e per base maggiore e base minore due intensità relative cumulate contigue. Si noti che il primo "trapezio" di fatto è un triangolo.
| area di massima concentrazione = 1•1/2 | 0,5 |
| area concentrazione = area di massima concentrazione-somma aree trapezi | 0,0530 |
| indice concentrazione = area concentrazione/area di massima concentrazione | 0,1060 |
| percentuale dell'area di massima concentrazione occupata dall'area di concentrazione | 10,6 % |
Calcolo automatico dell'indice di concentrazione
| valore centrale | frequenza | intensità | frequenza cumulata | intensità cumulata | frequenza relativa cumulata | intensità relativa cumulata | area trapezi |
somma aree trapezi | |||||||
area concentrazione=area di massima concentrazione-somma aree trapezi | |||||||
indice di concentrazione=area di concentrazione/area di massima concentrazione | |||||||
percentuale dell'area di massima concentrazione occupata dall'area di concentrazione | |||||||