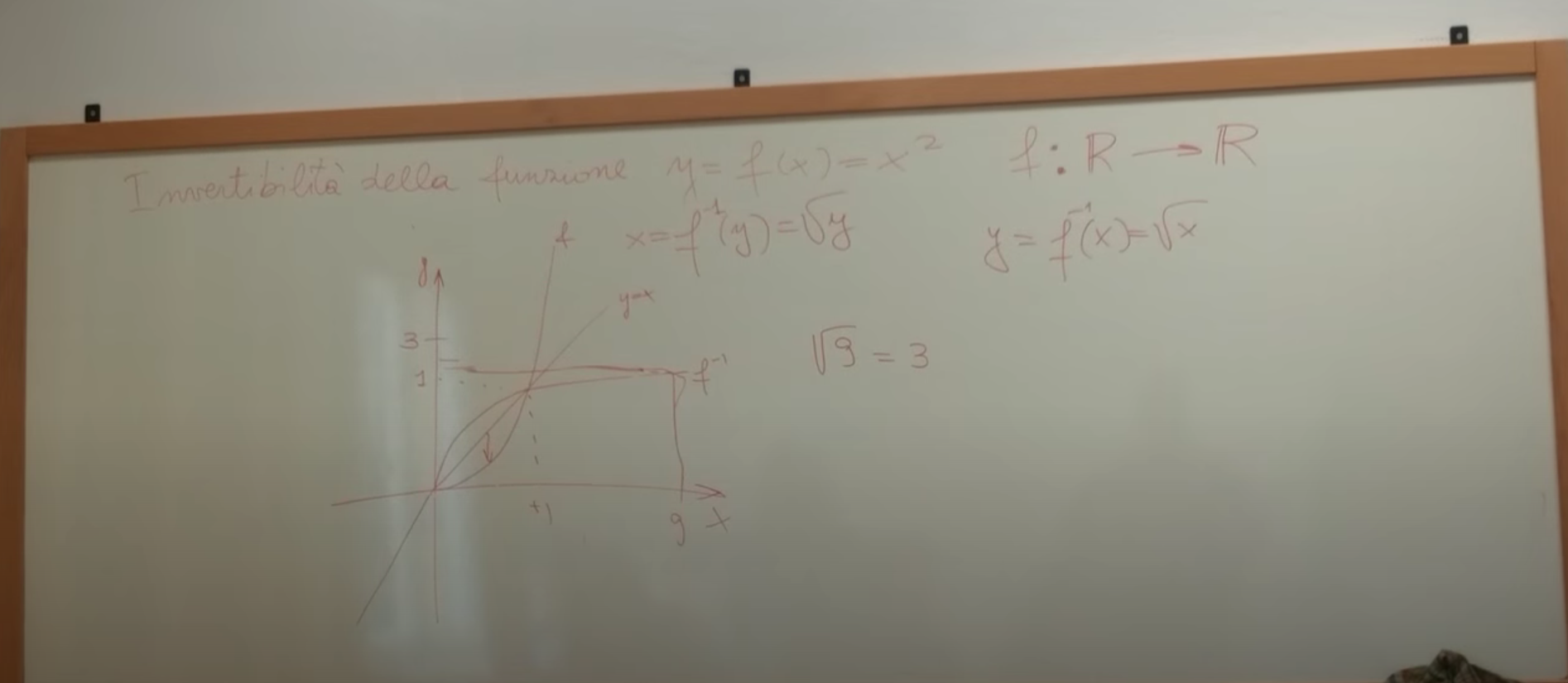Definizioni

Definizione: dati due insiemi non vuoti A e B chiamati rispettivamente dominio e codominio, si chiama relazione di A in B una legge che associa ad elementi di A, elementi di B.

Definizione: dati due insiemi non vuoti A e B chiamati rispettivamente dominio e codominio, si chiama funzione o applicazione di A in B, una relazione che associa ad ogni elemento di A, uno ed uno solo di B.

La funzione si indicherà f:A→B. Si dice che f è definita in A con valori in B. La x che denota il generico elemento di A si chiama la variabile. f(x) si dice immagine di x tramite la f.

Definizione: Il sottoinsieme del codominio costituito da gli elementi che sono i corrispondenti di qualche elemento del dominio si chiama insieme immagine della f.

L'insieme immagine della f si indicherà con f(A). Si noti che un elemento di B può anche non essere immagine di alcun elemento di A. Si noti ancora che un elemento di B può essere il corrispondente di più di un elemento di A.

Definizione: Dati due insiemi non vuoti A e B si dice prodotto cartesiano tra A e B, l'insieme delle coppie ordinate di cui il primo elemento appartiene ad A ed il cui secondo a B.

Il numero di coppie dell'insieme AxB è uguale al prodotto del numero degli elementi di A per il numero degli elementi di B.

Definizione: Il sottoinsieme del prodotto cartesiano AxB costituito da quelle coppie i cui elementi si corrispondono, tramite la funzione, si chiama grafico di f.

Il grafico di una funzione f lo indicheremo con G(f).

Proprietà

Definizione: La funzione f si dice suriettiva se f(A)=B.

Per formare applicazioni suriettive tra insiemi finiti, il numero di elementi del dominio dev'essere maggiore o uguale del numero di elementi del codominio.

Definizione: la funzione f si dice iniettiva se ogni elemento dell'insieme immagine proviene da un'unico elemento del dominio, ovvero da x≠y ne consegue che f(x)≠f(y).

Per formare applicazioni iniettive tra insiemi finiti, il numero di elementi del dominio dev'essere minore o uguale del numero di elementi del codominio.

Definizione: La funzione f si dice biettiva se risulta contemporaneamente sia iniettiva che suriettiva.

Per formare applicazioni biettive tra insiemi finiti, il numero di elementi del dominio dev'essere uguale del numero di elementi del codominio.

Definizione: La funzione f si dice costante se l'insieme immagine è costituito da un solo elemento.

Rappresentazione di relazioni e funzioni

Di seguito sono rappresentati i diagrammi sagittali e cartesiani, di alcune relazioni tra insiemi che contengono un numero finito di elementi.

Esempio 1

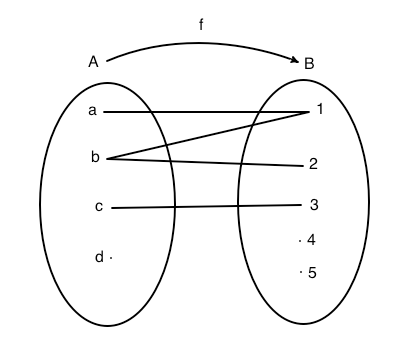
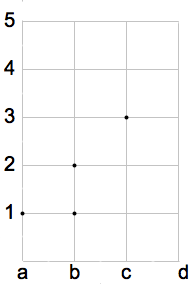
Ci sono due motivi per cui la relazione in figura non è una funzione. Nel diagramma sagittale a sinistra, lo si nota dal fatto che l'elemento b del dominio corrisponde a due elementi dell'insieme immagine cioè 1 e 2. Il secondo motivo è che l'elemento d non ha alcun corrispondente nell'insieme immagine. La definizione di funzione non è soddisfatta quindi si tratta di una semplice relazione. Nel diagramma cartesiano, a destra, il fatto che a b corrispondono i due valori 1 e 2 lo si nota perchè sulla verticale conotta da b ci sono due punti, inoltre, siccome sulla verticale condotta da d non si trova alcun punto si nota che d stesso non corrisponde ad alcun elemento dell'insieme immagine. Una relazione è funzione quando nel relativo diagramma cartesiano, su ogni verticale condotta dagli elementi del dominio c'è un'unico punto.

Esempio 2

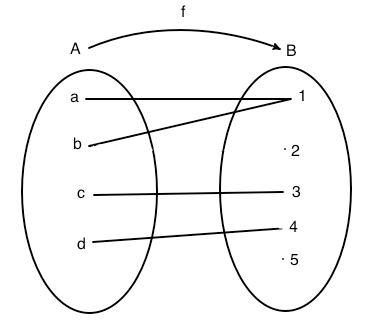
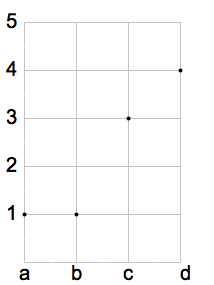
In figura è rappresenta una funzione senza particolari proprietà. L'insieme immagine è il sottoinsieme di B f(A)={1, 3, 4}. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,1), (c,3),( d,4)}. Nel diagramma cartesiano si nota che 2 e 5 non appartengono all'insieme immagine poichè sulle orizzontali condotte da questi due valori non c'è alcun punto.

Esempio 3

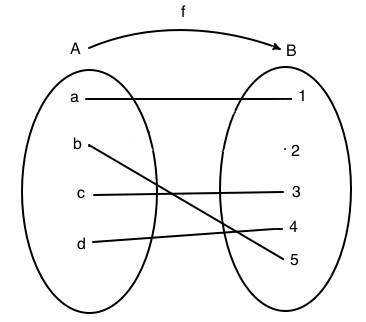
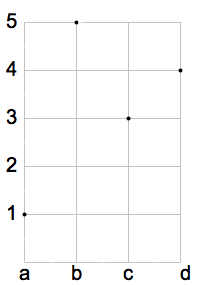
In figura è rappresenta una funzione iniettiva. Nel diagramma cartesiano si nota che su ogni orizzontale condotta dagli elementi del codominio c'è al massimo un punto. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,5), (c,3),( d,4)}.

Esempio 4

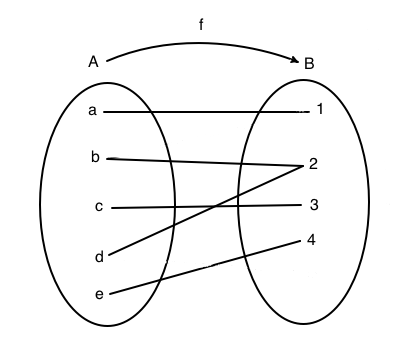
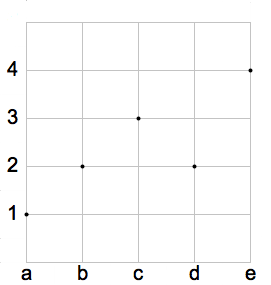
In figura è rappresenta una funzione suriettiva. Nel diagramma cartesiano si nota che su ogni orizzontale condotta dagli elementi del codominio c'è almeno un punto. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,2), (c,3),( d,2), (e,4)}.

Esempio 5

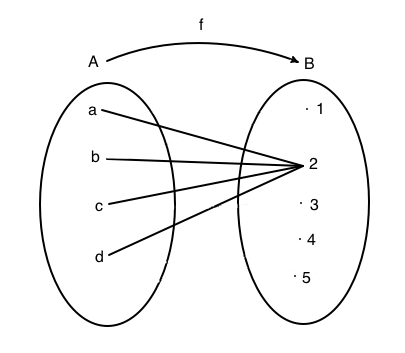
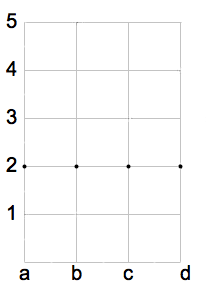
In figura è rappresenta una funzione costante. Nel diagramma cartesiano si nota che tutti i valori dell'insieme immagine stanno sulla stessa orizzontale. Il grafico della funzione è costituito dall'insieme: G(f)={(a,2), (b,2), (c,2),( d,2)}.

Esempio 6

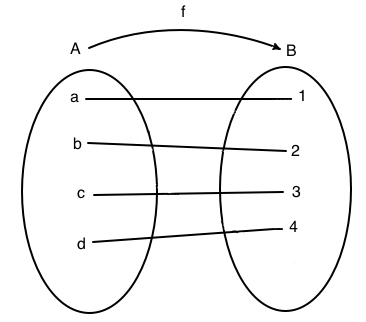
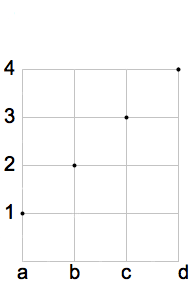
In figura è rappresenta una funzione biettiva. Nel diagramma cartesiano si nota che su ogni orizzontale c'è un unico punto. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,2), (c,3),( d,4)}.

Funzione composta

Nell'esempio presentato nella figura di sotto c'è una funzione h che ha valori in B ed una funzione g che assume valori in C, nell'ipotesi che l'insieme immagine della h sia contenuto nel dominio g si può considerare la funzione f che ha dominio in A e assume valori in C, ottenuta applicando in successione la funzione h e poi la funzione g.

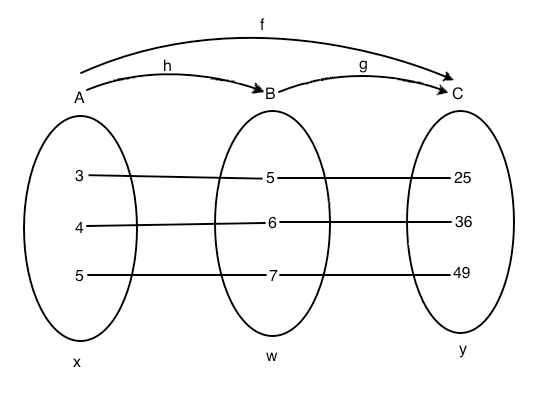
La funzione f così ottenuta si chiama funzione composta. La funzione composta può essere scritta in due modi diversi: f(x) = g(h(x)) oppure f(x) = (goh)(x). Si noti che nella notazione della funzione composta (goh)(x) è scritta prima la g e poi la h anche se prima si applica la h e poi la g.

In figura ci sono tre funzioni:

h: A→ B w = h(x) = x+2

g: B→ C y = g(w) = w²

f: A→ C y = f(x) = g(h(x)) = (goh)(x) = (x+2)²

La funzione h espressa a parole sarebbe "aggiungi 2", la g sarebbe "esegui il quadrato".

La funzione f è la composta di h con g.

L'operazione di composizione non gode della proprietà commutativa. Per dimostrare ciò basta trovare un controesempio. E' sufficiente quello presentato in figura, se si considera la h(g(x)) allora al numero 3 attraverso la g corrisponde il 9 ed al numero 9 attraverso la h corrisponde il numero 11, quindi h(g(3))=11 mentre g(h(3))=25, la funzione (hog)(x) infatti, ha la seguente espressione analitica y=x²+2 che non corrisponde con la (goh)(x)=(x+2)².

Funzione inversa

Problema diretto dato un insieme A di numeri si vuol costruire una funzione che li elevi al quadrato e quindi tolga tre. y=f(x)=x²-3 Problema inverso dato un insieme B di numeri si vuol costruire una funzione che aumenti i numeri di tre e quindi calcoli la radice. x=g(y)=√(x+3) Più in generale, per risolvere un certo problema, potrebbe essere importante saper individuare la funzione inversa cioè una funzione ottenuta scambiando dominio con codominio e che faccia corrispondere gli stessi elementi della funzione diretta. Da tener presente che se una funzione non è biettiva, l'inversa non è una funzione, ma una semplice relazione. Dunque le uniche funzioni invertibili sono quelle biettive.

La funzione inversa della f si indica con f^-1

Attenzione a non confondere questa notazione con quella della funzione reciproca 1/f

Se una funzione non è biettiva la si rende tale con delle opportune restrizioni che possono coinvolgere tanto il dominio che il codominio, ciò significa che si determina un sottoinsieme A' di A e un sottoinsieme B' di B tali che la f: A → B sia biettiva in tal modo si può considerare la f^-1: B' → A'

Una funzione f: A → B è l'inversa una funzione g: B → A se

g(f(x)) = x ∀ x ∈ A, e

f(g(y)) = y ∀ y ∈ B;

(gοf)(x) = i(x) dove con i(x) si è indicata la funzione identica

(fοg)(y)=i(y) dove con i(y) si è indicata la funzione identica

Invertibilità della funzione lineare

Data la funzione lineare y=f(x)=2x+1 f: Q → Q cerchiamo di individuare la relativa inversa. Per prima cosa ci si pone il problema di valutare se la funzione stessa è invertibile. La funzione lineare presa in esame, è biettiva, lo si nota poichè su ogni orizzontale c'è sempre solo un punto della funzione stessa. Essendo biettiva è invertibile, senza dover eseguire alcuna restrizione. La funzione inversa f^-1: R → R, ha quindi ancora l'insime Q per dominio e codominio. Per individuare l'espressione analitica dell'inversa dobbiamo esplicitare la variabile x ovvero -2x=-y+1 e dividendo per -2 si ottiene x=f^-1(y)=(y-1)/2. A questo punto per poter porre sullo stesso sistema di riferimento sia la f che la f^-1 rinominiamo le variabili ovvero y=f^-1(x)=(x-1)/2.

Notiamo che la f espressa a parole è: "moltiplica per 2 e somma 1". La f^-1 invece: "sottrai 1 e dividi il risultato per due". Si noti che per esprimere la f^-1 a parole basterebbe leggere da destra verso sinistra la f eseguendo però le operazioni inverse. In figura si noti che f e f^-1 sono simmetriche rispetto alla retta y=x questo perchè per disegnare la funzione inversa si sono dovuti ruotare gli assi cartesiani, sempre sulla retta y=x in modo da invertire l'asse delle x con quello delle y.

Invertibilità della funzione y=xⁿ

Data la funzione y=f(x)=xⁿ f: R → R, con n numero naturale, cerchiamo di individuare la relativa inversa. Per prima cosa ci si pone il problema di valutare se la funzione stessa è invertibile. A questo punto bisogna distinguere due casi. Se n è dispari La funzione presa in esame, é biettiva e quindi si può invertire su tutto R. Se invece n è pari non è biettiva, lo si nota poichè sulle orizzontali condotte sopra lo zero ci sono sempre due punti di intersezione con la funzione stessa, mentre sulle orizzontali condotte sotto lo zero non ci sono punti di intersezione con la funzione stessa. Non essendo quindi la funzione nè suriettiva nè iniettiva bisogna restringere sia il dominio che il codominio. Per rendere la funzione iniettiva si deve restringere il dominio a R₀⁺, in tal modo , infatti su ogni orizzontale ci sarà al massimo un solo punto di intersezione con la funzione. Per renderla anche suriettiva si deve restringere anche il codominio a R₀⁺, in tal modo , infatti su ogni orizzontale ci sarà al massimo un solo punto di intersezione con la funzione. Per individuare l'espressione analitica dell'inversa dobbiamo esplicitare la variabile x ottenendo quindi la radice ennesima di y ovvero, usando la notazione esponenziale, x=y^1/n. A questo punto per poter porre sullo stesso sistema di riferimento sia la f che la g rinominiamo le variabili ovvero y=g(x)=x^1/n.

Nella figura di sotto con lo slider si può modificare l'esponente n della f, da 2 a 9, da notare come cambia il dominio della funzione inversa g, a seconda se n è pari o dispari. La f e la relativa inversa g, sono simmetriche rispetto alla retta y=x, questo perchè per disegnare la funzione inversa si sono dovuti ruotare gli assi cartesiani, sempre sulla retta y=x in modo da invertire l'asse delle x con quello delle y. Si noti ancora che f, g hanno due punti di contatto ovvero l'origine e il punto (1;1) infatti 0²=0^1/2 e 1²=1^1/2. Prestiamo attenzione ancora al fatto che sarebbe sbagliato dire che, se n è numero pari, per esempio 2, √9=3 o anche √9=-3 perchè in questo caso a 9 corrisponderebbero due valori e quindi y=√x non sarebbe una funzione. Ovviamente a √9 è associato l'unico valore 3.

Grafico della funzione xⁿ, con n pari

Grafico della funzione xⁿ, con n dispari

Video lezione

Funzioni ed equazioni

Siano f(x) e g(x) due funzioni aventi uno stesso dominio A, se ciò non succede si assume A come intersezione dei domini di f e g. Ci si chiede se esistono dei valori appartenenti ad A per i quali le due funzioni risultano uguali, ovvero supponendo che le due funzioni siano espresse attrverso una rappresentazione analitica bisogna valutare se esistono dei valori appartenenti ad A tali che f(x)=g(x). Quella che abbiamo scritto è un'equazione con incognita x ed un valore s tale che f(s)=g(s) si chiama soluzione dell'equazione.