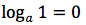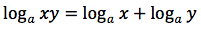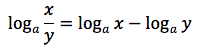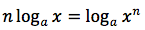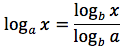Regole di derivazione
Per non dover calcolare ogni volta il limite per h tendente a zero del rapporto incrementale di funzioni si dimostrano di seguito le regole di derivazione. Una volta dimostrate, queste regole vengono utilizzate per facilitare la derivazione di funzioni di maggiore complessità.
Derivata della funzione somma
Ipotesi: siano f, g funzioni derivabili
Tesi: la funzione somma f+g è derivabile e si ha: (f+g)'=f'+g'
Dimostrazione: la funzione somma (f+g)(x) è, per definizione, uguale a f(x)+g(x), quindi il rapporto incrementale della g+f è dato da:
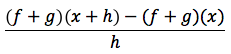
che per definizione può essere scritta anche così:
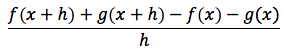
o anche così:
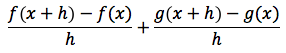
Per ottenere la derivata bisogna passare al limite per h tendente a zero ovvero ci si dovrà ricondurre al limite di una somma che è uguale alla somma dei limiti ovvero:
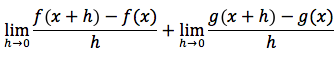
Tenendo conto che il limite del rapporto incrementale della f è f' e che il limite del rapporto incrementale della g è g' otterremo proprio la tesi.
Derivata della funzione prodotto
Ipotesi: siano f, g funzioni derivabili
Tesi: la funzione prodotto f*g è derivabile e si ha: (f*g)'=f'*g+f*g'
Dimostrazione: la funzione prodotto (f*g)(x) è, per definizione, uguale a f(x)*g(x), quindi il limite del rapporto incrementale per h tendente a zero della f*g è dato da:
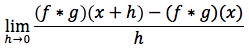
che per definizione è uguale a:
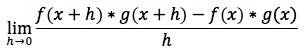
aggiungendo e togliendo dal numeratore il termine: f(x+h)*g(x) otteniamo l'espressione equivalente:
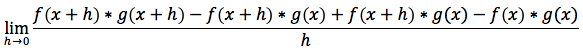
applicando i teoremi sui limiti questa espressione può essere scritta anche così:
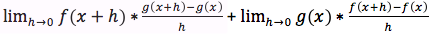
e quindi cosi'
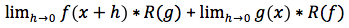
dove, con R(f), R(g) si intendono i rapporti incrementali delle funzioni f e g. Tenendo conto che il limite del prodotto è uguale al prodotto dei limiti, che g(x) e f(x) non dipendono dal tipi di incremento, otterremo proprio la tesi.
Derivata del prodotto di una costante per una funzione
Ipotesi: sia k una costante, sia f(x) una funzione derivabile
Tesi: la derivata di kf(x) = kf'(x)
Dimostrazione: applichiamo la formula della derivata di un prodotto: (kf(x))' = k'f(x) + kf'(x), la derivata di una costante k è però uguale a zero e quindi (kf(x))' = kf'(x) c.v.d.
Derivata di xn
Ipotesi: n sia un numero naturale
Tesi: La derivata di xn è uguale a nxn-1
Proviamo a derivare la funzione x2. Dovremo fare il limite per h tendente a zero del rapporto incrementale della funzione in oggetto. Il rapporto incrementale è:
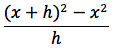
sviluppando otteniamo:
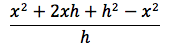
semplificando e raccogliendo il fattore h otteniamo il rapporto incrementale:
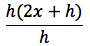
infine semplifichiamo il fattore h e passiamo al limite:
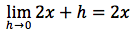
Proviamo ora a derivare la funzione x3. Analogamente al caso precedentemente trattato, dovremmo fare il limite per h tendente a zero del rapporto incrementale della funzione in oggetto. Il rapporto incrementale è:
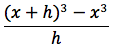
sviluppando otteniamo:
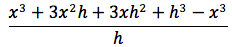
semplificando e raccogliendo il fattore h otteniamo il rapporto incrementale:
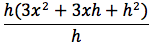
infine semplifichiamo il fattore h e passiamo al limite:
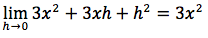
Riassumendo la derivata di x2 è 2x, la derivata di x3 è 3x2. Possiamo quindi prevedere che la derivata di xn sia uguale a nxn-1.
Dimostriamo ora che la derivata di xn è uguale a nxn-1 Per dimostrare questo teorema si applicherà il principio di induzione. Il principio consiste nel fatto che, se una proprietà è vera per n=1, supposto sia vera per n-1, se si dimostra che è vera anche per n allora è vera per ogni n appartenente ad N.
Gia' abbiamo verificato che il teorema vale per n=2, n=3, verifichiamo che il teorema vale anche per n=1:
Il rapporto incrementale della funzione y = x è:
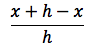
facendo il limite per h tendente a zero troviamo che tale limite è uguale a 1. Quindi si è dimostrato che la derivata della funzione x è 1 e quindi che il teorema è verificato per n=1. Supponiamo ora che la proposizione sia vera per n-1 ovvero (xn-1)'=(n-1)xn-2 e dimostriamo che è vera per n. Per derivare xn possiamo pensare che xn = xn-1 x, quindi per derivare xn applichiamo la formula della derivata di un prodotto:
(xn)' = (xn-1x)' = (xn-1)'x + xn-1(x)' = (n-1)xn-2x + xn-11 = (n-1)xn-1 + xn-1 = (n-1+1)xn-1 = nxn-1 c.v.d.
La formula non cambia se n assume valori negativi.
Per esercizio lo verifichiamo nel caso in cui n = - 1, in tal caso il rapporto incrementale è:
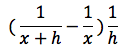
sviluppando si ottiene:
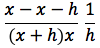
semplificando si ottiene:
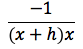
passando al limite per h tendente a zero si ottiene:
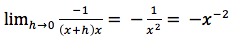
che è proprio quello che si voleva verificare.
La formula rimane tale e quale anche nel caso in cui l'esponente di x sia un numero razionale
Derivata di fn
Ipotesi: n sia un numero naturale, f sia una funzione derivabile.
Tesi: La derivata di fn è uguale a nfn-1f'.
Dimostrazione: Per dimostrare questo teorema si applicherà il principio di induzione. Il principio consiste nel fatto che, se una proprietà è vera per per un certo n, supposto sia vera per n-1, si dimostra che è vera per n, allora è vera per ogni n appartenente ad N.
Si può facilmente verificare che il teorema vale per n=2: basta pensare che f2=f*f ed applicare la regola della derivata del prodotto quindi (f*f)'=f'*f+f*f'=2f*f'.
Supponiamo ora che la proposizione sia vera per n-1 ovvero (fn-1)'=(n-1)fn-2f' e dimostriamo che è vera per n. Per derivare fn possiamo pensare che fn = fn-1f, quindi per derivare fn applichiamo la formula della derivata di un prodotto:
(fn)' = (fn-1f)' = (fn-1)'f +fn-1f' = (n-1)fn-2 f' + fn-1f' = (n-1)fn-1f' + fn-1f' = (n-1+1)fn-1f' = nfn-1f' c.v.d.
Si tenga presente che la formula è sempre valida anche nel caso in cui n sia un numero negativo o razionale.
Derivata del rapporto di due funzioni
Ipotesi: siano n(x) e d(x) due funzioni derivabili, d(x) sia diversa da zero nei punti in cui si vuol determinare la derivata.Tesi:
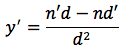
Dimostrazione:
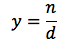
usando la notazione esponenziale si può scrivere:
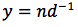
applichiamo la formula della derivata della funzione prodotto:
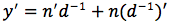
applichiamo la formula della derivata di fn con n=-1:
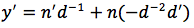
oppure usando la notazione di partenza si può anche scrivere:
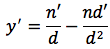
calcolando il minimo comune multiplo si può scrivere:
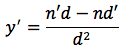
Derivata della funzione logaritmo
Tesi:
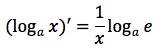
Dimostrazione: Il rapporto incrementale della funzione logaritmo e':
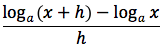
applicando la terza proprieta' del logaritmo possiamo scrivere cosi' il rapporto incrementale:
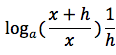
o anche cosi':
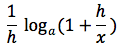
moltiplicando e dividendo per x possiamo scrivere cosi' il rapporto incrementale:
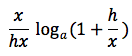
per la quarta proprieta' del logaritmo x/h lo portiamo all'esponente:
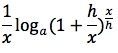
e infine applicando al rapporto incrementale il limite per h tendente a zero otteniamo:
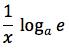
tenendo presente che con "e" si e' indicato il numero di Nepero. Per la proprietà 5 del logaritmo, che in pratica permette di fare un cambiamento di base si può anche scrivere:
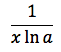
e se la base del logaritmo corrisponde proprio al numero di Nepero la derivata si trasforma in una una relazione molto semplice:
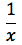
Derivata della funzione seno
Teorema: la derivata della funzione seno è la funzione coseno
Ipotesi: l'angolo x viene misurato in radiani
Tesi: sin'x=cosx
Dimostrazione: la derivata si otterrà con il limite per h tendente a zero del rapporto incrementale della funzione seno:
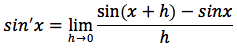
sappiamo che sin(x+h)=sinxcosh+cosxsinh per la formula di addizione del seno quindi possiamo scrivere:
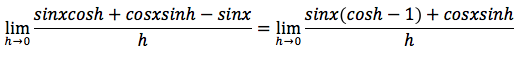
sapendo che il limite di una somma è uguale alla somma dei limiti possiamo scrivere:
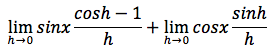
tenendo presente che valgono le seguenti relazioni:
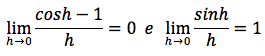
si deduce la tesi:
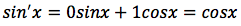
Derivata della funzione coseno
Teorema: la derivata della funzione coseno è la funzione -seno
Ipotesi: l'angolo x viene misurato in radiani
Tesi: cos'x=-sinx
Dimostrazione: la derivata si otterrà con il limite per h tendente a zero del rapporto incrementale della funzione coseno:
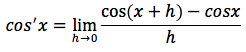
sappiamo che cos(x+h)=cosxcosh-sinxsinh per la formula di addizione del coseno quindi possiamo scrivere:
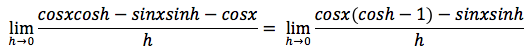
sapendo che il limite di una somma è uguale alla somma dei limiti possiamo scrivere:
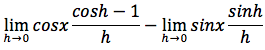
tenendo presente che valgono le seguenti relazioni:
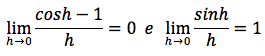
si deduce la tesi:
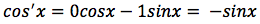
nota
La derivata della funzione -sinx è -cosx e la derivata della funzione -cosx è sinx quindi riassumendo:
sinx'=cosx
cosx'=-sinx
-sinx'=-cosx
-cosx'=sinx
In altre parole facendo per quattro volte la derivata della funzione seno ritroviamo la stessa funzione.
Derivata della funzione tangente
La funzione tangente può essere scritta come rapporto tra seno e coseno:
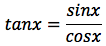
si applica la formula della derivata della funzione rapporto:
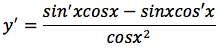
tenendo conto che sin'x=cosx e cos'x=-sinx otteniamo:
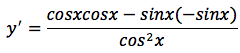
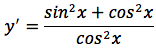
applicando il principio fondamentale della trigonometria: sin2x+cos2x=1, la derivata della funzione tangente può essere scritta in due modi diversi, ma tra loro equivalenti:
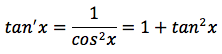
Derivata della funzione composta
Ipotesi: Siano date due funzioni derivabili in ogni punto del dominio:
y=g(x) g: A→B
z=f(y) g: B→C
supponiamo che, variando x nel dominio A, la funzione y=g(x) assuma valori appartenenti al dominio B della funzione f(y).
Allora le due funzioni date definiscono la funzione composta z=h(x)=f(g(x)), h: A→C
Tesi: La derivata della funzione composta h(x) è data dal prodotto delle derivate delle due funzioni: h'(x)=f'(y)*g'(x)
Dimostrazione: Il rapporto incrementale della funzione composta è:

Derivata della funzione inversa
Ipotesi: Sia y=f(x) una funzione reale a variabile reale x, continua e invertibile in un intervallo I, derivabile nel punto x ∈ I, con derivata f'(x) ≠ 0. Sia x=fi(y) la sua inversa.
Tesi: fi(y) è derivabile nel punto y=f(x) e si ha: fi'(y) =1/f'(x)
Dimostrazione: Se componiamo la fi(y) con la f(x), risulta: fi[f(x)]=x
derivando entrambi i membri di questa uguagliaza, applicando la regola di derivazione delle funzioni composte si ottiene:
fi'(y) *f'(x) = 1
da questa relazione, essendo per ipotesi f'(x) ≠ 0, si ricava la tesi
Derivata di y=arcsinx
La funzione y=fi(x)=arcsinx può scritta come funzione inversa di x=siny, quindi si può applicare la formula della derivata della funzione inversa. Nel primo passaggio la derivata di siny è cosy nel secondo passaggio si è tenuto presente la proprietà fondamentle della trigonometria sin2y+cos2y=1, nell'ultimo passaggio si è tenuto conto che x=siny.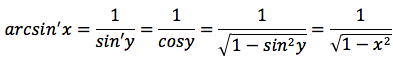
Derivata di arcosx
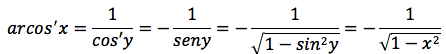
Derivata di arctanx
La funzione y=fi(x)=arctanx può scritta come funzione inversa di x=tany, quindi si può applicare la formula della derivata della funzione inversa. Nell'ultimo passaggio si è tenuto conto che x=tany.
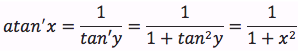
Derivata di ax
La funzione y=fi(x)=ax può scritta come funzione inversa di x=logay, quindi si può applicare la formula della derivata della funzione inversa. Nell'ultimo passaggio si è tenuto conto che y=ax
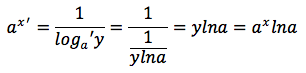
Derivata di ex
Se la base della funzione esponenziale è il numero di Nepero e allora lne=1 quindi applicando la formula precedente si ha che:
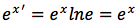
Si può concludere dicendo che la derivata della funzione ex è uguale alla funzione stessa.