Studio di funzioni

Studiare una funzione significa determinare gli elementi che la caratterizzano per poterla graficare, a partire dalla sua espressione analitica y=f(x).

Tracciatori di funzione

Tracciatore di funzione e tangente

Traccia funzioni razionali. Si possono tracciare funzioni con numeratore e denominatore fino al terzo grado. Con n₀, n₁, n₂, n₃, si sono indicati i coefficienti, rispettivamente di grado 0,1,2,3 del numeratore, con d₀, d₁, d₂, d₃, si sono indicati i coefficienti, rispettivamente di grado 0,1,2,3 del denominatore. Con gli slider si possono impostare, con incremento unitario, i coefficienti da -9 a +9. Spostando il punto A, si determina l'equazione della relativa tangente.

Tracciatore di funzione irrazionale

Traccia funzioni con numeratore e denominatore fino al quarto grado. Traccia asintoti verticali ed obliqui. Traccia parabole asintotiche purchè la differenza tra il grado del numeratore e quello del denominatore sia pari a due. Traccia cubiche asintotiche purchè la differenza tra il grado del numeratore e quello del denominatore sia pari a tre. Si può modificare tramite gli slider en, ed, l'esponente dell'intera funzione, sempre con incremento unitario. Il numeratore, en, varia da -1 a +3, il denominatore, ed, da 0 a 3. Si può visualizzare quindi la radice quadrata e cubica, della funzione, si può visualizzare la funzione elevata al quadrato e al cubo. Ponendo en=-1, ed=1 si può determinare anche la funzione reciproca.

Traccia valore assoluto di funzioni

Traccia funzioni razionali con numeratore e denominatore fino al terzo grado. Spostando lo slider su 0.5 si può visualizzare la funzione in valore assoluto.

Definizioni

Massimo assoluto

x₀ è punto di massimo assoluto se f(x₀) risulta essere maggiore di f(x) per ogni x appartenente al dominio della funzione.

Minimo assoluto

x₀ è punto di minimo assoluto se f(x₀) risulta essere minore di f(x) per ogni x appartenente al dominio della funzione.

Punto di massimo relativo

x₀ è punto di massimo relativo se esiste un intorno di x₀ dove, per ogni valore di x, f(x₀) risulta essere maggiore di f(x).

Punto di minimo relativo

x₀ è punto di minimo relativo se esiste un intorno di x₀ dove, per ogni valore di x, f(x₀) risuta essere minore di f(x).

Convessità

Una funzione f è convessa in un punto x₀ se esiste un intorno di x₀ in cui il grafico di f si trova tutto al di sopra della tangente alla curva nel punto x₀.

Concavità

Una funzione f è concava in un punto x₀ se esiste un intorno di x₀ in cui il grafico di f si trova tutto al di sotto della tangente alla curva nel punto x₀.

Punto di flesso

Un punto di flesso e' un punto dove la curva cambia di concavità.

Tra flessi si possono distinguere quelli ascendenti, dove la funzione e' concava a sinistra e convessa a destra, e flessi discendenti dove la funzione è convessa a sinistra e concava a destra.

Punto di flesso orizzontale

Diremo che un flesso e' orizzontale quando la tangente del flesso e' orizzontale.

Data una curva mediante la sua equazione cartesiana y=f(x), per disegnarne il grafico e determinandone le principali proprietà, procediamo ad analizzare i seguenti punti:

Dominio

Per quanto riguarda il dominio o campo di esistenza, se non viene assegnato, bisogna calcolarlo in base all'espressione analitica della funzione stessa. Questa espressione analitica può contenere operazioni come somma, prodotto, quoziente, radici, potenze, logaritmi .... e quindi occorre determinare l'insieme dei numeri reali per i quali hanno senso tutte le operazioni (o funzioni) presenti.

Studio del segno

Per studiare il segno della funzione, cioè per valutare quando la funzione è positiva o negativa bisogna determinare quali sono i valori della x appartenenti al dominio che soddisfano le disequazioni f(x)<0, f(x)>0. A questo punto conviene tratteggiare sul piano cartesiano tutte le zone in cui non si sviluppa il grafico della funzione, se ad esempio nell'intervallo [a,b] la funzione risultasse positiva si tratteggia la zona del piano sotto l'asse x.

Simmetrie

Si possono presentarsi i seguenti tipi di simmetrie. Se ∀ x ∈ dominio, f(x)=f(-x), allora la funzione è simmetrica rispetto all'asse y, in questo caso si dice che la funzione è pari. Per disegnarne il grafico sarà sufficiente studiare la funzione nel primo e quarto quadrante, per poi ruotare il grafico intorno all'asse y, facendo quindi corrispondere ad ascisse opposte la stessa ordinata. Se ∀ x ∈ dominio, f(-x)=-f(x), allora la funzione è simmetrica rispetto all'origine degli assi, in tal caso si dice che la funzione è dispari. Sarà sufficiente disegnare il grafico della funzione nel primo e quarto quadrante, per poi attraverso una simmetria centrata nell'origine riportare il grafico nel terzo e quarto quadrante, facendo corrispondere ad ascisse opposte, ordinate opposte.

Se si verifica che f(x)=f(x+P) ∀ x ∈ dominio allora si dirà che una funzione sia periodica di un certo periodo P, in tal caso sarà sufficiente studiare la funzione nell'intervallo chiuso [0,P], per poi ricopiare il grafico in tutti gli intervalli desiderati [ kP,kP+P ] con k∈N.

Asintoti

Una curva è detta asintoto di una funzione se la distanza di un punto della funzione dalla curva tende a zero quando l'ascissa o l'ordinata del punto tendono all'infinito. Se la curva è una retta orizzontale, l'asintoto si dirà asintoto orizzontale. Se la curva è una retta verticale, l'asintoto si dirà asintoto verticale. Se la curva è una retta obliqua, l'asintoto si dirà asintoto obliquo. Se la curva è una parabola, l'asintoto si dirà parabola asintotica.

Limiti

Per determinare l'andamento della funzione occorre calcolare i limiti negli estremi del campo di esistenza, più precisamente se D è l'unione di un numero finito di intervalli disgiunti I₁, I₂ ..... I_n, si tratta di calcolare i valori che la funzione assume negli estremi di I₁, I₂ ..... I_n e se la funzione non è definita in questi estremi vedere se esiste il limite, calcolandone il valore quando x tende a questi estremi.

Punti di discontinuità

Vista la definizione, una funzione risulta continua in x₀ dove assume il valore finito f(x₀) se valgono queste tre condizioni:

1. esiste limite destro finito per x tendente ad x₀

2. esiste limite sinistro finito per x tendente ad x₀

3. Il limite destro è uguale al limite sinistro ed è uguale a f(x₀)

Una funzione è discontinua in un punto se in quel punto viene meno una delle tre condizioni per la continuità.

Discontinuità di primo tipo: se il limite sx è diverso da quello dx e sono entrambi finiti, allora la discontinuità sarà di primo tipo e la differenza in valore assoluto tra i 2 limiti si dirà salto della funzione

Discontinuità di secondo tipo: se uno dei 2 limiti (DX o SX) non esiste o è infinito allora la discontinuità sarà di secondo tipo.

Discontinuità di terzo tipo: quando il valore assunto dalla funzione è diverso dal limite oppure quando c'è un "buco" ovvero non esiste la funzione in quel punto.

Punti particolari

Può essere utile, individuare alcuni punti del piano che appartengono al grafico della funzione, in particolare le eventuali intersezioni con gli assi cartesiani. Per individuare le intersezioni con l'asse x bisogna risolvere l'equazione f(x) = 0. Risolvendo l'equazione, si possono presentare i seguenti casi: o l'equazione non ha soluzioni allora il grafico della funzione non interseca l'asse x; oppure l'equazione presenta un numero finito di soluzioni in questo caso il grafico ha un numero finito di punti di intersezione con l'asse x; oppure ancora l'equazione ha infinite soluzioni per cui il grafico della funzione ha infiniti punti di intersezione con l'asse x. Per quanto riguarda invece l'eventuale intersezione con l'asse y, esiste ed è unica solamente se lo zero appartiene al dominio della funzione. Questo perchè, per definizione di funzione, su ogni verticale può starci al massimo un punto. Basterà quindi sostituire a x il valore zero e la eventuale soluzione sarà il punto di coordinate (0,f(0)).

Studio derivata prima

Per avere un'indicazione precisa sull'andamento del grafico sarà la determinazione degli intervalli dove la funzione risulta crescente o decrescente. Se la funzione sarà derivabile sarà il segno della derivata a dirci esattamente come si comporterà la funzione da questo punto di vista. Più precisamente la f sarà crescente negli intervalli dove la f' sarà positiva e decrescente in quelli dove f' sarà negativa. Per questo motivo si dovrà studiare l'equazione f'(x)=0 e la disequazione f'(x)>0, che saranno importanti per la ricerca dei punti di massimo e minimo relativi.

Studio derivata seconda

Per avere un'indicazione precisa sui flessi e sull'andamento della concavità e convessità di una funzione ci verrà in aiuto il seguente teorema (senza dimostrazione): se una funzione f è dotata di derivata prima e seconda in tutti i punti di un intervallo aperto di estremi A, B allora, se f''(x₀)>0, f(x) è convessa in x₀, se f''(x₀)<0, f(x) è concava in x₀. Se f''(x₀)=0 avremo un flesso che sarà crescente o decrescente in relazione al segno della derivata terza e cioè se f'''(x₀)>0, avremo un flesso crescente, se f'''(x₀)<0, avremo un flesso decrescente.

Conclusioni

A questo punto bisogna fare un riepilogo delle informazioni ottenute, magari completandole con qualche nuova osservazione. E' importante avere una conoscenza globale sul comportamento di una funzione, perché ciò ci potrà permettere di fare delle verifiche su dei calcoli già compiuti. Se per esempio un certo limite in x₀ assumesse un valore positivo, ma lo studio del segno ci dicesse che in x₀ la funzione assume un valore negativo sarebbe evidente che qualche calcolo non è stato fatto in modo corretto e che quindi si deve procedere a trovare gli errori.

Funzioni polinomiali

Le funzioni polinomiali y=f(x) si chiamano così in quanto f(x) è un polinomio. Una funzione polinomiale potrà essere scritta in questo modo:

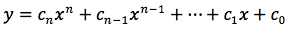
Il campo di esistenza è R

Non ci sono asintoti

Studio del segno: risolvendo la disequazione f(x)>0 si troveranno gli eventuali intervalli dove la funzione stessa risulterà positiva, la funzione risulterà negativa nell'insieme complementare.

Mettendo a sistema l'equazione della funzione, con l'equazione degli assi: (y=0 asse ascisse, x=0 asse delle ordinate) e risolvendo i due sistemi si otterranno gli eventuali punti di intersezione della funzione con gli assi.

Attraverso lo studio della derivata sarà possibile individuare gli eventuali intervalli dove la funzione risulta crescente o decrescente e dove ci saranno eventuali punti di massimo minimo o flesso.

Attraverso lo studio della derivata seconda sarà possibile individuare eventuali punti di flesso.

Funzioni razionali

Una funzione razionale è di questo tipo:

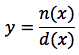
dove n e d sono rispettivamente due polinomi, più precisamente può essere scritta così:

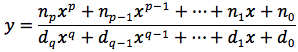
dove n_i e d_i sono rispettivamente i coefficienti del numeratore e del denominatore, p e q rispettivamente i gradi del numeratore e del denominatore.

Per determinare il dominio o campo di esistenza della funzione, bisogna escludere i valori nei quali si annulla il denominatore

Studio del segno: risolvendo la disequazione f(x)>0 si troveranno gli eventuali intervalli dove la funzione stessa risulterà positiva, la funzione risulterà negativa nell'insieme complementare.

Asintoti: In ogni punto dove si annulla il denominatore ci sarà un asintoto verticale a meno che in quel punto non si annulli pure il numeratore, in quest'ultimo caso potrebbe esserci un cosìdetto punto di discontinuità di terza specie, dal punto di vista grafico un "buco" della funzione. La funzione razionale f(x) si presenta come rapporto di due polinomi f(x)=n(x)/d(x). Se eseguiamo la divisione tra numeratore e denominatore troviamo un certo quoziente q(x) ed un certo resto r(x). Il grado del quoziente sarà: grado(q) = grado(n) - grado(d), il grado del resto dovrà minore del grado del denominatore d. A questo punto potremo scrivere che n:d=q, con resto r e di conseguenza n=qd+r. Dividendo entrambi i membri dell'ultima relazione scritta per d otteniamo:

In altre parole la nostra funzione razionale può essere scritta come somma del quoziente con l'altra funzione razionale r/d. Tenendo presente che in r/d il grado di r è minore del grado di d, il limite per x tendente all'infinito sarà uguale zero. A questo punto possiamo pensare che per x tendente ad infinito, la funzione razionale n/d tende a q, q allora sarà per definizione l'asintoto di n/d. Quindi se q è di grado zero ed è zero ci sarà un asintoto corrispondente all'asse delle ascisse, se q è di grado zero ma è un numero diverso da zero, ci sarà un asintoto orizzontale non coincidente all'asse delle ascisse, se q è di grado uno ci sarà per asintoto una retta obliqua, se q è di grado due ci sarà una parabola asintotica ecc... ecc... Quindi se, per esempio, il grado del numeratore è tre ed il grado del denominatore è due, la differenza dei gradi tra numeratore e denominatore è uno. Uno sarà quindi il grado dell'asintoto e quindi la funzione razionale avrà per asintoto una retta obliqua.

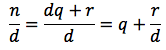
Limiti "indicativi": si dovranno calcolare i limiti per x tendente a più infinito e meno infinito per capire come si comporta la funzione in questi due casi e i limiti dovranno confermare quello che si è calcolato nel punto precedente riguardante gli asintoti. Dovranno essere calcolati quindi i limiti per x tendente ai punti nei quali la funzione non è definita e queti limiti dovranno confermare quello quello che si è ottenuto calcolando gli asintoti verticali.

Attraverso lo studio della derivata sarà possibile individuare gli eventuali intervalli dove la funzione risulta crescente o decrescente, se ci saranno punti di massimo minimo o flesso.

Esempio 1 di funzione razionale

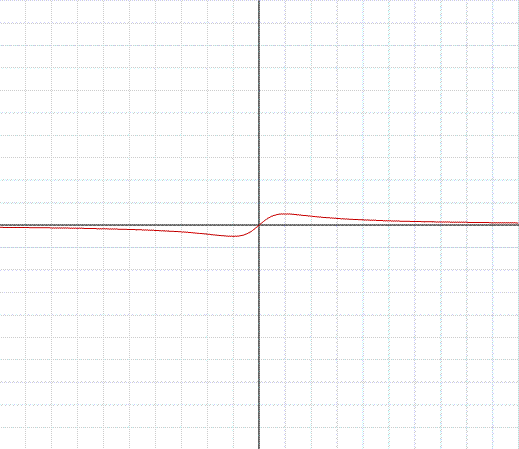
Nell'esempio in figura, il grafico della funzione razionale:

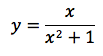
Il dominio di questa funzione è l'intero insieme R dei numeri reali, in quanto il denominatore non si annulla mai. Notiamo che il numeratore è di primo grado e il denominatore di secondo. Eseguendo la divisione tra numeratore e denominatore troviamo che il quoziente è zero appunto perchè il grado del denominatore è maggiore del grado del numeratore. Il quoziente della divisione è l'asintoto della funzione, in questo esempio quindi l'asintoto è la retta y=0 che corrisponde, come si nota dal grafico, all'asse delle ascisse. Si noti ancora che la funzione è definita per ogni valore reale, questo perchè il denominatore non si annulla per alcun valore reale.

La derivata prima è: f'=(1-x²)/(x²+1)². Attraverso lo studio del segno di f' si ottengono un punto di massimo relativo in (1,1/2) ed un punto di minimo relativo in (-1,-1/2). La derivata seconda è: f''=(2x(x²-3)/(x+1)³. Attraverso lo studio del segno di f'' si ottengono due punti di flesso decrescente in (-√3,√3/4) e in (√3,√3/4) e un flesso crescente nel punto (0,0).

Esempio 2 di funzione razionale

Nell'esempio in figura, il grafico della funzione razionale:

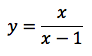
Notiamo che sia il numeratore che il denominatore sono di primo grado. Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di grado zero, che in pratica è il numero ottenuto dividendo i coefficienti n₁/d₁ che nello specifico corrisponde al numero 1. La retta di equazione y=1 è l'asintoto della funzione, quindi asintoto orizzontale. Tale risultato è confermato pure dal primo limite "indicativo" calcolato sotto.

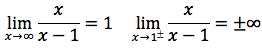
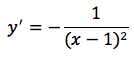
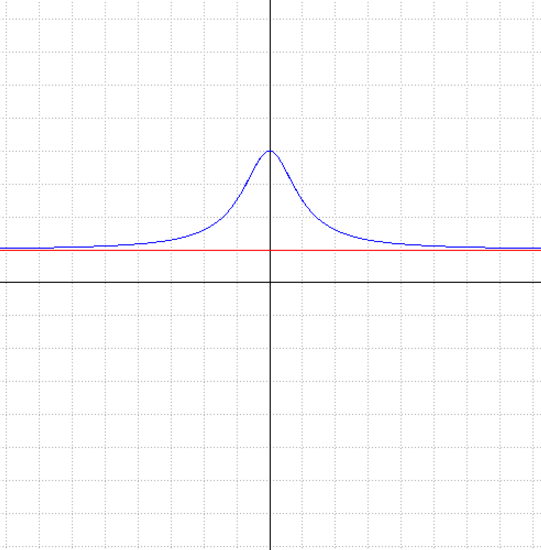
Si tenga conto che la funzione ha pure un asintoto verticale x=1 nel punto dove si annulla il denominatore e tale conclusione è conseguenza del secondo limite "indicativo". Il punto 1 è un punto di discontinuità di seconda specie. La derivata, calcolata sotto, risulta negativa per ogni valore reale, quindi, la funzione risulta sempre decrescente.

Esempio 3 di funzione razionale

Nell'esempio in figura, il grafico della funzione razionale:

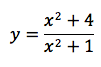
Notiamo che sia il numeratore che il denominatore sono di secondo grado. Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di grado zero, che in pratica è il numero ottenuto dividendo i coefficienti n₁/d₁ che nello specifico corrisponde al numero 1. La retta di equazione y=1 è l'asintoto della funzione, quindi asintoto orizzontale. Un limite indicativo è quello calcolato di sotto e che conferma l'esistenza dell'asintoto orizzontale

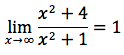
Si tenga conto che la funzione non ha asintoti verticali in quanto il denominatore risulta diverso da zero per ogni valore reale.

Attraverso lo studio del segno della derivata che è la funzione:

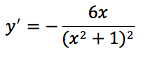
e ponendo la derivata uguale a zero, si determina un massimo relativo M di coordinate M(0;4).

Esempio 4 di funzione razionale

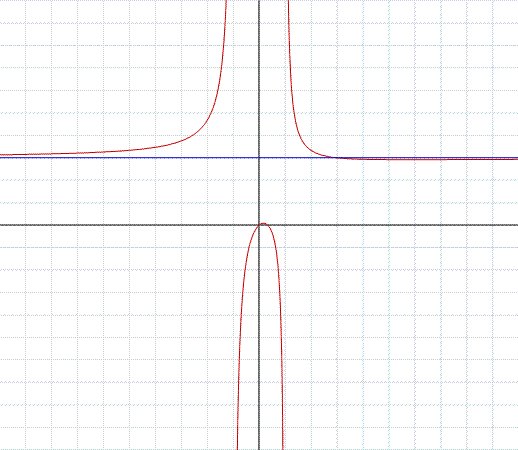
Nell'esempio in figura, il grafico della funzione razionale:

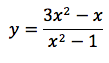
Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di grado zero, che in pratica è il numero ottenuto dividendo i coefficienti n₂/d₂ e nello specifico corrisponde al numero 3. La retta di equazione y=3 è l'asintoto orizzontale della funzione. Il primo limite "indicativo" conferma ciò che siè detto riguardo l'asintoto orizzontale.

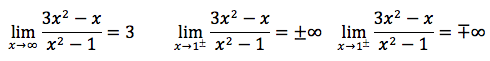
Si noti ancora che la funzione ha pure gli asintoti verticali x=1 x=-1, nei punti dove si annulla il denominatore. Gli ultimi due limiti indicativi confermano ciò che si è detto riguardo gli asintoti verticali. Uguagliando a zero la derivata, troviamo un massimo ed un minimo relativi rispettivamente nei punti di ascissa sotto indicati.

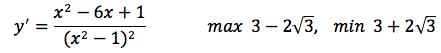
Esempio 5 di funzione razionale

Nell'esempio in figura, il grafico della funzione razionale:

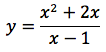
Notiamo che il numeratore è di secondo grado e il denominatore di primo. Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di primo grado, esattamente: x+3. La retta di equazione y=x+3 è quindi asintoto obliquo della funzione. Si noti ancora che la funzione ha pure l'asintoto verticale x=1 nel punto dove si annulla il denominatore. Il punto 1 è un punto di discontinuità di seconda specie.

Uguagliando a zero la derivata che è la funzione:

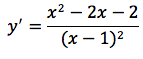
troviamo un massimo ed un minimo relativi rispettivamente nei punti di ascissa:

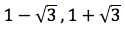
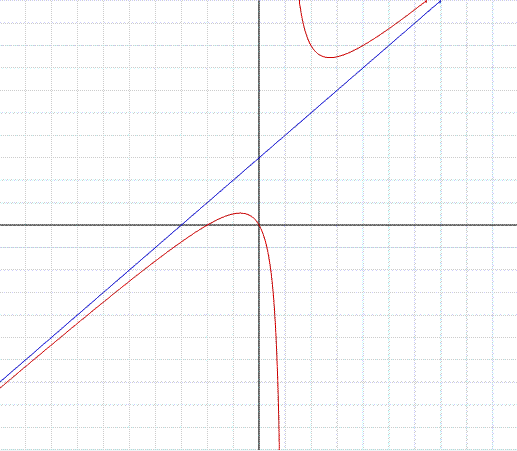
Esempio 6 di funzione razionale

Nell'esempio in figura, il grafico della funzione razionale:

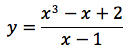
Il dominio è l'insieme dei numeri reali tranne il punto dove si annulla il denominatore, in simboli: ∀ x ∈ R\{1}. Notiamo che numeratore e denominatore sono rispettivamente di terzo e primo grado. Eseguendo la divisione tra numeratore e denominatore troviamo il quoziente di secondo grado, blu in figura:

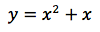
che è l'asintoto della funzione, ovvero una parabola asintotica. Tale risultato è compatibile con il terzo limite "indicativo" calcolato sotto. Si noti ancora che la funzione ha l'asintoto verticale x=1 nel punto dove si annulla il denominatore. Tale asintoto si trova eseguendo il limite per x tendente a uno, tale valore è un punto di discontinuità di seconda specie.

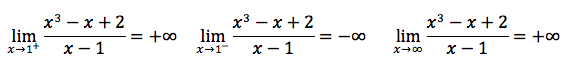
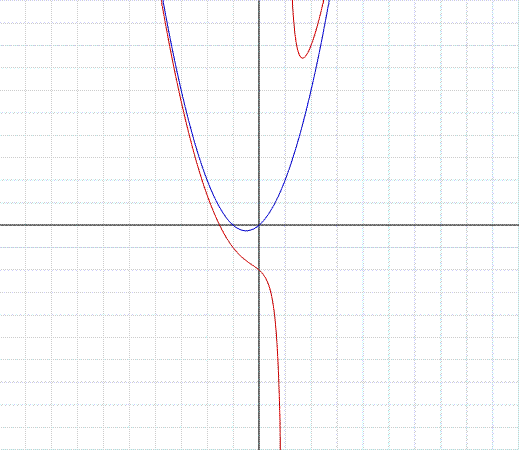
Esempio 7 di funzione razionale

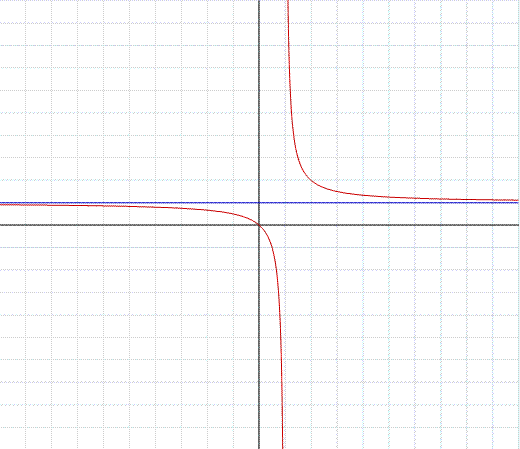
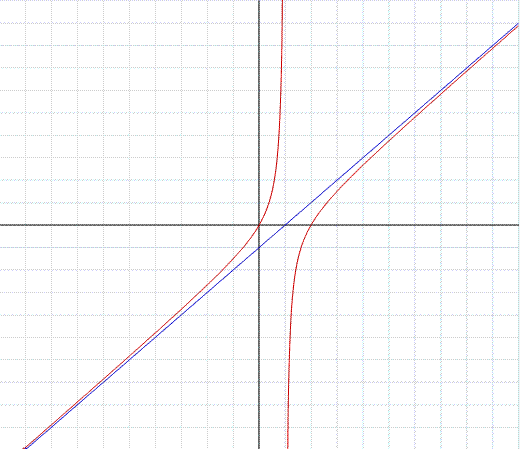
Nell'esempio in figura, il grafico della funzione:

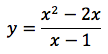
Il dominio è l'insieme dei numeri reali tranne il punto 1 dove si annulla il denominatore. Eseguendo il limite per x tendente a uno ovvero, precisando i limiti destro e sinistro,

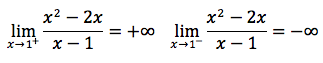
Si deduce che c'è un asintoto verticale di equazione x=1. Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente di primo grado, ovvero la retta di equazione y=x-1 che è dunque l'asintoto obliquo della funzione. La derivata risulta la funzione calcolata sotto e tenendo presente che è sempre positiva, la funzione, come si nota dal grafico, è sempre crescente.

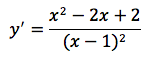
Funzioni irrazionali

Una funzione si dice irrazionale se nella relativa espressione analitica, la variabile indipendente x sta "sotto" ad una radice. Analizzeremo, in particolare, funzioni irrazionali di questo tipo:

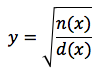
ovvero si tratta di una funzione razionale posta all'interno di una radice quadrata. Supponiamo di conoscere il grafico di questa funzione razionale e cerchiamo di valutare come una radice quadrata può "modificarlo".

Come si modifica il grafico di una funzione se viene posta sotto radice

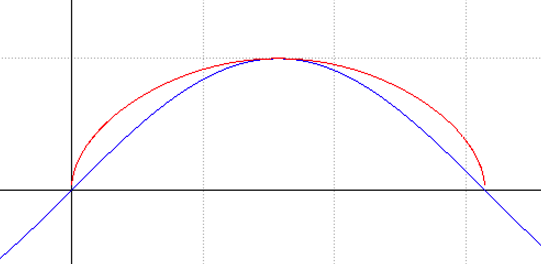
In figura sono messi a confronto i grafici di una retta e quello della stessa retta posta sotto la radice:

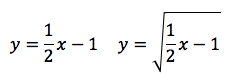
Sono messe a confronto, quindi due funzioni che "differiscono" per una radice quadrata. Teniamo presente che una radice quadrata è impossibile in R quando l'argomento della radice stessa assume valori negativi. Ne consegue che, dove la funzione è negativa, la funzione sotto radice non ha dominio. La funzione, del tipo considerato, ha valori reali solamente quando la funzione, senza la radice, si sviluppa al di sopra dell'asse x.

Notiamo ancora che: la radice quadrata "cala" i valori maggiori di 1, e "solleva" i valori minori di 1, lascia inalterato il valore 1. Tutto ciò lo si può verificare sul grafico, in quanto l'orizzontale y=1 interseca entrambe le funzioni mentre sopra la retta y=1 la funzione irrazionale in nero "cala" rispetto alla funzione razionale in blu, sotto la retta y=1 la funzione irrazionale si "solleva" rispetto alla funzione razionale. Infatti la radice di 4 "cala" e diventa 2, perchè 4 è un numero maggiore di 1, la radice di 0,49 si "solleva" a 0,7 infatti 0,49 è un numero minore di 1. La radice di 1 rimane sempre 1.

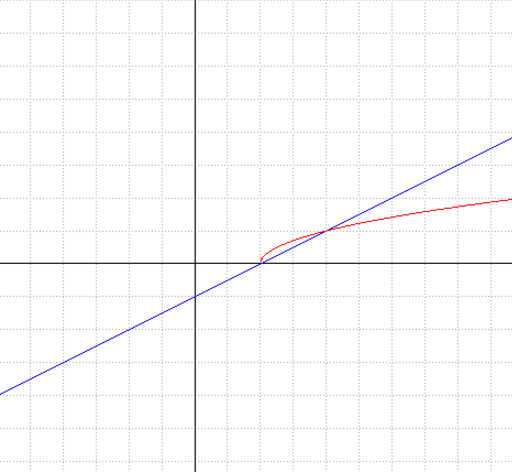
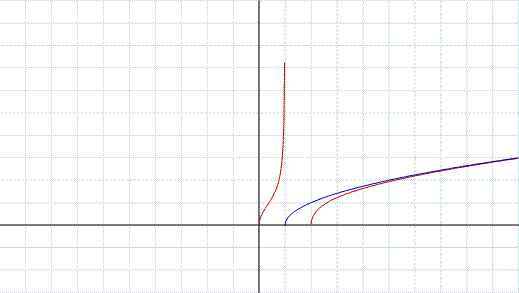
La funzione razionale presa in esame nel grafico, in blu, a destra, è la stessa trattata nell'esempio 7 visto in precedenza.

Il grafico di tale funzione, in blu, viene messo a confronto con quello quello della stessa funzione posta sotto la radice che nel grafico è di colore marron.

Le espressioni analitiche delle due funzioni quindi, sono le seguenti:

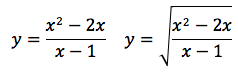
Dal grafico si nota che per i valori dove la funzione in blu risulta negativa, la funzione posta sotto radice non è definita.

Si può notare ancora che al di sotto del valore 1 la funzione in marron, ovvero la funzione sotto radice, viene "sollevata" e sopra il valore 1 viene "abbassata", rispetto alla funzione di partenza.

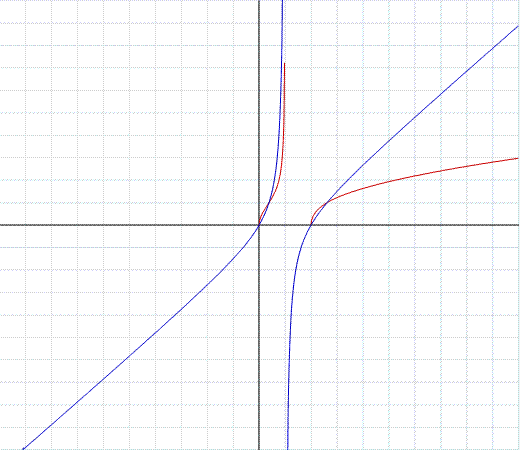
Teniamo presente che la funzione razionale:

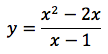
per asintoto la retta y=x-1, ne consegue che la funzione irrazionale (in colore marron):

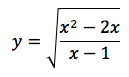
ha per asintoto la curva in blu:

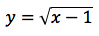
In figura sono messi a confronto i grafici, ristretti ad un certo intervallo, della funzione seno, in blu, e quello della stessa funzione posta sotto la radice che nel grafico è di color marron:

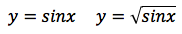
Anche in questo esempio sono messe a confronto, due funzioni che "differiscono" per una radice quadrata.

Teniamo presente che, dove la funzione seno è negativa, la funzione sotto radice non ha dominio.

Notiamo anche in questo esempio che la radice quadrata "solleva" i valori minori di 1