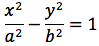Maths e-book
Geometria analitica
Geometria analitica
Il percorso storico che portò a non considerare algebra e geometria due discipline distinte è dovuto all'opera di René Descartes (La Haye en Touraine (oggi Descartes), 1596 - Stoccolma, 1650), noto anche col nome italianizzato di Cartesio, filosofo, scienziato e matematico francese. Descartes affrontò la geometria con gli strumenti dell'algebra, facendo corrispondere ai punti del piano coppie ordinate di numeri reali. Le coppie ordinate di numeri reali portano proprio il nome di prodotto cartesiano e vengono indicate con R x R. Nel sistema di riferimento che prende il nome di piano cartesiano, viene a crearsi una corrispondenza biunivoca tra equazioni algebriche e figure geometriche come rette, parabole, circonferenze, ellissi.
Cartesio tentò di applicare alla filosofia il metodo deduttivo della matematica, cercò di dubitare di tutto, tranne che della propria esistenza, egli stesso nell'atto del pensare doveva esistere. Cartesio espresse questa conclusione nel famoso motto: "Cogito, ergo sum".
Per individuare un punto su una retta va fissato innanzitutto il verso di percorrenza. Il verso normalmente, se la retta è orizzontale, va da sinistra verso destra, se è verticale va dal basso verso l'alto. Va fissata inoltre un'origine e va precisata l'unità di misura. Va creata quindi una corrispondenza biunivoca tra punti della retta e numeri reali in modo che ad ogni punto della retta sia associata la sua distanza dall'origine. L'origine deve corrispondere con lo zero e i punti associati ai numeri positivi, sono quelli che seguono l'origine, quelli associati ai numeri negativi precedono l'origine.
La distanza tra due punti A e B su una retta, che indicheremo con d(A,B), corrisponde alla lunghezza del segmento AB. La distanza tra due punti A, B deve corrispondere quindi, ad un numero reale positivo. Conoscendo le coordinate dei due punti A e B, per individuare la misura del segmento AB va fatta la sottrazione tra il valore maggiore e quello minore tra le due coordinate. Per esempio per determinare la distanza tra A(-3) e B(2) si esegue la sottrazione 2-(-3)=5 quindi d(A,B)=5. Più in generale, per scrivere una formula che rimanga comunque valida senza dover distinguere quale tra i due valori è il maggiore si introduce nella formula della distanza il valore assoluto ovvero d(A,B)=|xA-xB|
Dati due punti A, B su una retta indichiamo con M il punto medio del segmento AB. Il punto M è quindi quel punto tale che d(A,M)=d(B,M). Indicate con xA e xB le coordinate di A e B vogliamo determinare la coordinata di M. La distanza d(A,B) è data dalla differenza tra la coordinata maggiore B e quella minore A ovvero xB-xA. La distanza d(A,M) sarà data quindi dalla (xB-xA)/2. Per determinare quindi la coordinata di M si dovrà sommare alla coordinata di A, che è il valore minore la d(A,M), oppure si dovrà sottrarre alla coordinata di B, che è il valore maggiore la d(A,M) ovvero:
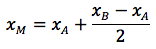
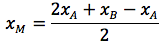
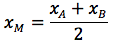
Come detto, i punti della retta sono in corrispondenza biunivoca con un numero reale, nel caso del piano ogni punto può essere messo in corrispondenza biunivoca ad una coppia ordinata di numeri reali. Per individuare un punto nel piano si fa uso di un sistema di riferimento composto da due rette perpendicolari, una orizzontale ed una verticale. L'origine del sistema di riferimento corrisponde all'intersezione delle due rette che si chiamano rispettivamente, l'asse delle orizzontali: asse delle ascisse o asse delle "x" e l'asse delle verticali: asse delle ordinate o asse delle "y". Fissata l'unità di misura, in generale la stessa per entrambi gli assi, per esempio il punto A può essere messo in corrispondenza biunivoca con la coppia ordinata (5;8), infatti il punto A si trova all'incrocio della verticale condotta dal punto 5, con l'orizzontale condotta dal punto 8. I valori 5 e 8 sono chiamati rispettivamente ascissa ed ordinata del punto A. Tale sistema di riferimento è detto riferimento cartesiano ortogonale.
La distanza nel piano è una applicazione che associa ad ogni coppia di punti del piano un valore reale che per ogni terna A,B,C di punti soddisfa alle seguenti proprietà:
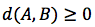
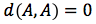
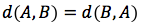
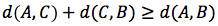
Si vuol determinare la lunghezza del segmento AB ovvero la distanza tra due punti A e B rispettivamente di coordinate A(xA;yA) B(xB;yB). Si applichi il teorema di pitagora al triangolo ABC
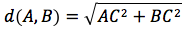
Siccome d(A,C)=|yA-yB| e d(B,C)=|xA-xB| si sostituisce ottenendo:
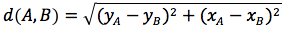
Si noti ancora che scrivere (xA-xB)2 o (xB-xA)2 è la stessa cosa.
Si chiama luogo geometrico di equazione f(x,y)=0, l'insieme di tutti e soli i punti del piano che godono della proprietà che le rispettive coordinate sostituite alle incognite x e y, dell'equazione, verificano l'equazione stessa.
L'asse di un segmento è il luogo geometrico costituito dall'insieme di tutti e soli i punti del piano che hanno la proprietà di essere equidistanti dagli estremi del segmento.
Supponiamo di voler determinare l'equazione dell'asse del segmento di estremi A(xA;yA) e B(xB;yB)
Imponiamo che la distanza di un punto generico dell'asse P(x;y) da A e B siano uguali:
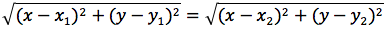
quadrando si ottiene:
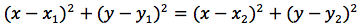
Sviluppando si ottiene:
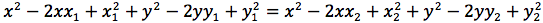
e semplificando si ottiene l'equazione dell'asse che è la retta perpendicolare al segmento passante per il suo punto medio:
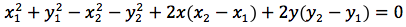
Esplicitiamo la y:
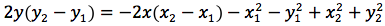
Tenendo conto che A e B sono punti distinti quindi y2-y1≠0, dividiamo entrambi i membri per y2-y1 e si ottiene:
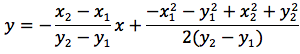
Si tratta di un'equazione di primo grado nelle incognite x e y, si noti infatti che x1, y1, x2, y2 sono semplici numeri reali.
Per ricavare l'equazione di una retta si considerino due suoi punti, P(x1, y1) e Q(x2, y2) e si individui il punto R(0,q), di intersezione della retta con l'asse delle ordinate. Se la retta passa per l'origine, q sarà uguale a zero. Si considerino i due triangoli rettangoli, PQT e RPS.
I due triangoli presi in considerazione sono simili essendo triangoli rettangoli, e avendo anche gli altri due angoli uguali. I loro cateti sono in proporzione quindi vale la relazione:
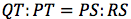
ovvero
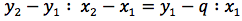
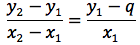
Il rapporto tra l'incremento delle ordinate, Δy e l'incremento delle ascisse, Δx si chiama coefficiente angolare m=Δy/Δx. Se, come per esempio in figura, m=2/3 allora per ogni incremento delle x di 3 il relativo incremento delle y è 2, dunque
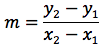
m è un parametro molto importante poichè da tale valore dipende l'inclinazione della retta. Se m è positivo la retta sarà crescente, se m è negativo decrescente, se m=0 la retta non sarà nè crescente nè decrescente e quindi orizzontale. Proseguendo, sostituiamo m ottenendo:
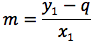
ricaviamo y1
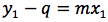ovvero
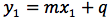
Abbiamo ricavato y1 in funzione di x1 pensando che P può essere un qualsiasi punto sulla retta di coordinate generiche P(x;y) otteniamo l'equazione della retta:
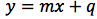
Si tratta di un'equazione di primo grado a due incognite. Il calcolo dell'equazione dell'asse di un segmento è in linea con questo risultato.
L'equazione di una retta passante per l'origine è del tipo: y=mx in tal caso infatti il punto R in figura, corrisponde con l'origine del sistema di riferimento e quindi q=0.
L'asse delle "x" è costituita da punti che hanno l'ordinata nulla mentre l'ascissa varia su tutto l'insieme dei numeri reali R, quindi l'equazione y=0 rappresenta l'asse delle "x" e x=0 l'asse delle "y". Analogamente, i punti delle rette parallele ad uno dei due assi hanno una coordinata costante mentre l'altra varia sull'insieme R. Indicando con k il valore di questa costante, le loro equazioni risultano quindi: y=k per le rette parallele all'asse delle ascisse, oppure x=k per le rette parallele all'asse delle ordinate.
Un'equazione di primo grado a due incognite è un'equazione indeterminata e ha quindi infinite soluzioni. Una soluzione è costituita da una coppia ordinata di numeri reali, tutte le infinite soluzioni dell'equazione, costituiscono le coordinate dei punti della retta. La retta è quindi il luogo geometrico i cui punti rappresentano le soluzioni di un'equazione di primo grado a due incognite. Le equazioni di primo grado a due incognite per questo motivo vengono anche dette equazioni lineari. L'appartenenza di un punto ad una retta o, più in generale ad un luogo geometrico può essere verificata sostituendo le coordinate del punto nell'equazione che rappresenta il luogo stesso, se l'equazione è verificata il punto appartiene al luogo, altrimenti non vi appartiene. In generale, dato che l'intersezione tra due luoghi geometrici è costituita da tutti e soli i punti soddisfacenti le equazioni di entrambi, il metodo di mettere a sistema queste equazioni per individuare i punti comuni ai due luoghi è del tutto generale e vale per qualunque curva. Se questo sistema è impossibile i luoghi geometrici non hanno punti in comune, mentre se esso ammette soluzioni ad ogni soluzione corrisponde un punto in comune.
Un fascio di rette si dice proprio se ogni sua retta passa per lo stesso punto, detto centro del fascio.
Per determinare l'equazione del fascio di centro il punto C(3;2), si considera l'equazione della retta generica: y=mx+q e siccome la retta deve passare per C è necessario che le coordinate di C soddisfino l'equazione, dunque: 2=3m+q, ricaviamo q in funzione di m: q=-3m+2 e sostituiamo tale risultato, nell'equazione generica della retta: y=mx-3m+2 raccogliamo m ottenendo: y=m(x-3)+2 che possiamo anche scrivere: y-2=m(x-3). Al variare di m otteniamo tutte le rette passanti per C, tranne l'equazione della parallela all'asse delle ordinate, ovvero la retta verticale passante per C che ha equazione x=3. Più in generale dato un punto C(x1;y1) l'equazione del fascio di centro C é del tipo: y-y1=m(x-x1) al variare di m si ottengono tutte le rette passanti per C tranne che la retta di equazione x=x1.
Un fascio di rette si dice improprio se le sue rette sono tutte parallele tra loro.
Per determinare l'equazione del fascio improprio di rette parallele alla retta di coefficiente angolare -2 basta far variare il termine noto q, quindi y=-2x+q rappresenta l'equazione di un fascio improprio di rette.
Si considerino i due punti, P(x1, y1) e Q(x2, y2). Dato che per due punti passa una ed una sola retta, ne vogliamo determinare l'equazione. La retta deve appartenere al fascio proprio di centro P ovvero:
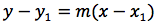
Il coefficiente angolare di una retta, come visto è dato da:
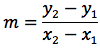
Sostituendo nell'equazione del fascio
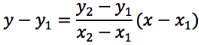
tenendo conto che P e Q sono punti distinti quindi y2-y1≠0, dividiamo entrambi i membri per y2-y1 e otteniamo così l'equazione della retta passante per due punti:
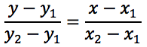
All'inizio del capitolo, si è dimostrato che una retta si rappresenta tramite un'equazione del tipo y=mx+q. Dimostriamo ora che vale anche il viceversa, ossia che nel piano cartesiano, un'equazione di primo grado a due incognite, rappresenta una retta. Partendo dall'equazione y=mx+q si possono determinare due punti del luogo geometrico dando per esempio a x i valori 1 e 2 ottenendo così i punti A(1;m+q) e B(2;2m+q). Se applichiamo la formula della retta passante per due punti ad A e B, semplici calcoli ci portano ovviamente a ricavare l'equazione y=mx+q, abbiamo dimostrato quindi che l'equazione di una retta passante per A e B è quella di partenza.
Supponiamo di avere due rette nel piano r: ax+by+c=0, r': a'x+b'y+c'=0. Mettiamo a sistema le equazioni che rappresentano le due rette. Il sistema corrispondente può avere un'unica soluzione se le rette sono incidenti, infinite soluzioni se esse sono coincidenti oppure nessuna soluzione se esse sono parallele e distinte. Per valutare le condizioni di parallelismo analizziamo in modo più dettagliato le situazioni che vengono a crearsi:
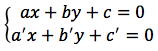
Il sistema è possibile, ovvero le rette sono incidenti, se vale la seguente condizione:
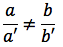
Il sistema è indeterminato, ovvero le rette sono sovrapposte, se vale la seguente condizione:
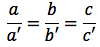
Il sistema è ipossibile, ovvero le rette sono parallele, se vale la seguente condizione:
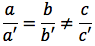
Dalla relazione di sopra si ottiene:
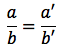
Partendo dall'equazione:
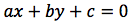
Partendo dall'equazione:
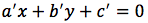
esplicitiamo la y:
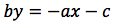
esplicitiamo la y:
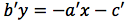
otteniamo:
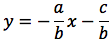
otteniamo:
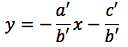
Notiamo che i coefficienti angolare delle due rette prese in considerazione sono rispettivamente m=-a/b, m'=-a'/b' e nell'ultima relazione, si è visto che, nel caso delle rette parallele, a/b=a'/b'. Si è ottenuto quindi il risultato che se due rette sono parallele allora hanno lo stesso coefficiente angolare. Viceversa se due rette hanno lo stesso coefficiente angolare, ma termine noto diverso allora appartengono allo stesso fascio improprio e sono quindi parallele. Possiamo dedurre la relazione di parallelismo tra le rette ovvero:
Due rette sono parallele se e solo se i relativi coefficienti angolari sono uguali.
Si è visto che l'equazione della retta passante per A(x1;y1) e B(x2;y2) è del seguente tipo:
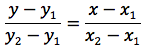
Esplicitando la y si ottiene:
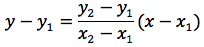
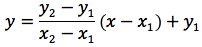
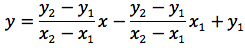
Si è visto anche qual'è l'equazione dell'asse del segmento AB ovvero:
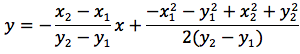
Teniamo presente che le ultime due equazioni rappresentano due rette che sono tra di loro perpendicolari. Indicando con m il coefficiente angolare della retta AB e con m' il coefficiente angolare dell'asse del segmento AB, si noti che uno è opposto e reciproco dell'altro.
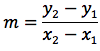
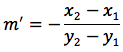
Viceversa si può dimostrare che due rette aventi equazioni con i coefficienti angolari opposti e reciproci sono perpendicolari. Per far ciò si può individuare su una delle due rette un segmento in modo che l'altra retta intersechi il suo punto medio. A questo punto si dimostra che tale retta costituisce l'asse del segmento verificando che un suo punto generico è equidistante dagli estremi del segmento.
Supponiamo, per esempio, di avere le due rette r: y=3x+1, r': y=-(1/3)x+13/3, si noti che i rispettivi coefficienti angolari sono opposti e reciproci, dimostriamo che le rette sono perpendicolari. Mettendo a sistema le due rette si determina la soluzione (1;4) che corrisponde alle coordinate del punto Q di intersezione delle due rette. Prendiamo sull'asse delle x due punti equidistanti dal punto 1 che rappresenta l'ascissa di Q, per esempio 0 e 2. Se nell'equazione della retta r' sostituiamo a x il valore 0 troviamo che la relativa y vale 1, se nelle stessa equazione sostituiamo a x il valore 2 troviamo che la relativa y vale 7. In tal modo abbiamo individuato sulla retta r' due punti A(0;1) e B(2;7) equidistanti da Q(1;4). Ora basta verificare che il punto generico P della retta r' è equidistante da A e da B. Il punto generico della retta r' ha coordinate: P(x;-(1/3)x+13/3), calcoliamo le distanze d(P;A) e d(P;B).
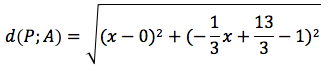
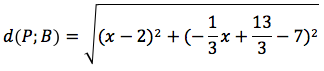
Sviluppando le rispettive formule delle due distanze otteniamo che danno lo stesso risultato:
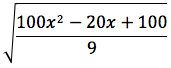
In tal modo abbiamo dimostrato che il punto generico P della retta r' risulta essere equidistante da A e B, per questo r' è l'asse del segmeto AB e siccome il segmento AB sta sulla retta r', abbiamo dimostrato che r è perpendicolare ad r'.
Basterebbe ora riproporre la stessa verifica per due rette di equazioni generiche sempre con i coefficienti angolari opposti e reciproci e dimostrare che una può essere l'asse di un particolare segmento che appartiene all'altra retta.
Per calcolare la distanza di un punto P di coordinate (x1, y1) da una retta r di equazione y = m x + q si determina il fascio di rette di centro P (x1, y1). Si sostituisce al coefficiente angolare m il valore -1/m, in modo che la retta risultante sia perpendicolare a quella assegnata. Si determini il punto punto di intersezione delle rette mettendo a sistema le due equazioni. Infine si calcoli la distanza tra il punto di intersezione trovato e quello di coordinate (x1, y1). Dalla procedura vista si può anche ricavare una formula che che consenta di calcolare direttamente la distanza di un punto da una retta. Tuttavia, un'applicazione consapevole della procedura, seppur laboriosa, appare più utile per imparare ad interconnettere alcuni concetti importanti e per questa ragione, tale formula non viene calcolata.
Supponiamo di avere una retta a, ed una retta g incidente ad a . Supponiamo che l'angolo formato dalle due rette non sia retto.
Il "cono circolare retto a due falde" è definito come la superficie generata dalla rotazione della retta g, che è chiamata generatrice, intorno alla retta a che costituisce quindi l'asse di rotazione.
Il punto V di intersezione tra a e g è detto "vertice" del cono.
L'angolo α formato da g con a è detto "semiapertura" del cono.
Il cono è, per come è stato definito, un cono infinito, a due falde, unite per il vertice. La parte di cono compresa tra il vertice e una sezione si chiama cono finito.
Se la sezione è normale, si definisce cono finito retto.
Se la retta generatrice è parallela all'asse, la superficie ottenuta si chiama "cilindro circolare retto"
Il cilindro può essere considerato come un particolare cono, in tal caso il vertice stà all'infinito.
Si chiamano coniche non degeneri le curve che si ottengono intersecando una superficie conica con un piano non passante per il vertice del cono.
Si chiamano coniche degeneri le curve che si ottengono intersecando una superficie conica con un piano passante per il vertice del cono.
Una conica è la curva ottenuta intersecando un cono circolare retto con un piano.
Chiamiamo x l'angolo formato dal piano secante con la retta generatrice e con α la semiapertura del cono, distinguiamo i seguenti tipi di coniche: circonferenze, ellissi, parabole ed iperboli si distinguono a seconda di come è disposto il piano che seziona il cono.
Se prendiamo un piano passante per il vertice otteniamo una cosiddetta conica degenere. Vediamo ora i vari casi possibili di sezioni coniche degeneri. Pensiamo innanzitutto di sezionare un cilindro, che come si è visto, può essere pensato come un particolare cono. Il piano non taglia il cilindro: non si ottiene nessuna conica reale. Il piano taglia il cilindro ed è parallelo all'asse di rotazione: conica degenere in due rette distinte parallele.
E' ottenuta dall'intersezione del cono con un piano che ha l'angolo x=0, perpendicolare quindi al suo asse. La circonferenza è una curva chiusa ed è una contenuta in una sola delle due falde del cono. La circonferenza degenere si riduce ad un solo punto, il vertice.
E' ottenuta intersecando il cono con un piano, che con il suo asse formi un angolo compreso tra: α⟨x⟨π/2. L'ellisse è una curva contenuta in una sola delle due falde del cono ed è una curva chiusa. L'ellisse degenere si riduce ad un solo punto, il vertice.
E' ottenuta per intersezione del cono con un piano che ha l'angolo x=α, parallelo quindi alla retta generatrice. La parabola appartiene a una sola delle falde del cono e non è una curva chiusa. La parabola degenere si riduce a due rette coincidenti in quanto il piano che seziona il cono, passando per il vertice ed essendo parallelo alla generatrice, risulta tangente al cono.
E' ottenuta per intersezione del cono con un piano che formi con il suo asse un angolo compreso tra: α⟨x≤π/2. L'iperbole è una curva aperta ed appartiene ad entrambe le falde del cono, in quanto il piano le interseca. L'iperbole degenere si riduce ad una coppia distinta di rette incidenti nel vertice che risultano essere due generatrici del cono.
Le equazioni di secondo grado in due incognite sono costituite da una somma di sei termini:
ax2+bxy+cy2+dx+ey+f=0Queste equazioni sono di diversi tipi, alcune non ammettono soluzioni reali, altre ammettono solo una soluzione, altre ancora sono indeterminate e ammettono infinite soluzioni. Tenendo presente che una soluzione è una coppia ordinata di valori, riportando nel piano cartesiano queste coppie ordinate, otteniamo dei punti che costituiscono una conica.
Le coniche degeneri come quelle non degeneri, riferite ad un sistema di assi cartesiani ortogonali, si esprimono dunque, mediante funzioni algebriche di secondo grado. L'aspetto algebrico delle coniche degeneri, iperboli e parabole, risulta il prodotto di due equazioni di primo grado. L'equazione di un'iperbole degenere si avrà moltiplicando membro a membro le equazioni sotto forma implicita delle due rette incidenti nel vertice; Es. Le due rette di equazione x=0, y=0, costituiscono l'iperbole degenere di equazione xy=0 l'equazione di una parabola degenere si ottiene innalzando al quadrato i due membri dell'equazione, in forma implicita, della retta. La retta di equazione 2x+4y-1=0 presa due volte dà luogo alla parabola degenere (2x+4y-1)²=0 L'equazione di un'ellisse degenere è data da quella di un'ellisse che si riduce ad un solo punto. L'ellisse di equazione x2+2y2=0 corrisponde all'origine Segnaliamo ora alcuni esempi di coniche degeneri, dopo aver ricordato che dal punto di vista analitico una conica è degenere se l'equazione che la rappresenta è soddisfatta da un unico punto reale (esempio 3x2 + 5y2 = 0) oppure se il polinomio che la individua è scomponibile.
1) Conica degenere in due rette reali distinte x (x+y) = 0 (tipo iperbolico) (x - 1 ) ( x + 1) = 0 (tipo parabolico) 2) conica degenere in due rette reali coincidenti (x + y +1)(x + y + 1) = 0 Segnaliamo ora un esempio di conica completamente immaginaria: 3x2 + 4y2 = -1 Ovviamente non esiste alcuna coppia di numeri reali (x;y) che soddisfa l'equazione. Ripetiamo che tale conica è detta ellisse immaginaria perchè, come vedremo, rientra nel tipo ellittico.Le equazioni di secondo grado in due incognite hanno diverse sfacettature, alcune non ammettono soluzioni reali come x2+xy+y2+4=0, altre ammettono solo una soluzione x2+y2=0, altre, come per esempio come x2+4xy+4y2-9=0 sono date dal prodotto tra due rette (x+2y+3)(x+2y-3)=0. Altre equazioni sono indeterminate ovvero ammettono infinite soluzioni, tenendo sempre presente che una soluzione è una coppia ordinata di valori, riportando nel piano cartesiano queste coppie ordinate, otteniamo dei punti che costituiscono una conica.
Tutto ciò è in accordo con il fatto che se intersechiamo un cono a due falde con un piano passante per l'asse di simmetria, si determinano due rette, se il piano passa per il vertice del cono si determina un solo punto, se il piano contiene la generatrice del cono si determina una retta corrispondente proprio alla generatrice e queste sono dette coniche degeneri.La conica di equazione ax2+bxy+cy2+dx+ey+f=0
é una parabola, eventualmente degenere in due rette parallele se: b2-4ac=0 é un'ellisse (eventualmente immaginaria oppure degenere in un punto) se: b2-4ac<0 é una'iperbole, eventualmente degenere in due rette incidenti se: b2-4ac > 0.OSSERVAZIONE Una conica é quindi una parabola (eventualmente degenere in due rette parallele) se e solo se il complesso dei termini di secondo grado é un quadrato perfetto; una parabola ha quindi equazione del tipo
(ax+by)2+cx+dy+e=0
Si dimostra che la retta di equazione ax+by = 0 é parallela all'asse della parabola. Essendo l'equazione di una conica individuata da 5 parametri una conica generica sara' individuata da 5 punti il ciò equivale a dire che per 5 punti passa una ed una sola conica Essendo l'equazione di una conica non tanto semplici da trattare, alcune coniche si studiano in posizioni particolari: come ad esempio le ellissi con asse orizzontale o le parabole con asse verticaleDal punto di vista fisico, l'orbita descritta da una particella carica che entra in un campo magnetico uniforme è una circonferenza.
Dal punto di vista fisico l'orbita descritta da un pianeta è un'ellisse, per esempio la terra, ruotando attorno al sole descrive un'ellisse in cui, il sole stesso, corrisponde ad uno dei due fuochi. I moti dei pianeti avvengono quindi su un piano, detto piano orbitale.
Dal punto di vista fisico la parabola è la traiettoria a cui è costretto un proiettile, soggetto alla forza gravitazionale.
Dal punto di vista fisico se un corpo arriva nella sfera gravitazionale di un pianeta con una velocità sufficientemente elevata, si allontana seguendo una traiettoria iperbolica di cui il pianeta stesso rappresenta il fuoco.
C'è una definizione che accomuna tutte le coniche (non degeneri). Dato un punto F, fuoco ed una retta d, direttrice, non contenente F, chiamata d(F;P) la distanza di un punto P della conica dal fuoco e chiamata d(H;P) la distanza del punto P della direttrice
Conica è il luogo geometrico del piano costituita dai punti P tali che che il rapporto d(F;P)/d(P;H) è costante
tale costante "e" si chiama eccentricità della conica.
Per e = 0 si ottiene una circonferenza
Per 0 < e < 1 si ottiene un'ellisse
Per e = 1 una parabola
per e > 1 una iperbole.
Da questa definizione generale di conica basata sull'eccentricità si può dimostrare che ne conseguono le definizioni specifiche di conica che vedremo in seguito.
L'equivalenza fra la definizione delle coniche come intersezioni nello spazio di un cono circolare retto a due falde con un piano e la loro definizione come luoghi geometrici nel piano è stato chiarito dal matematico parigino Germinal Pierre Dandelin, attraverso un teorema che porta il suo nome. Dandelin nacque in pieno periodo rivoluzionarionato (1794-1847) e combattè per Napoleone, durante i cento giorni lavorò per il Ministero degli Interni agli ordini di Lazare Carnot. Dopo la sconfitta di Napoleone a Waterloo nel 1815 si rifugiò nel Belgio e nel 1817 diventò cittadino olandese.
Per una ellisse e una iperbole si possono assumere due coppie fuoco, direttrice, da cui deriva la stessa curva.
Nel caso della circonferenza e = 0 e si deve immaginare che la retta direttrice sia a distanza infinita dal fuoco.
Il caso della circonferenza va trattato come caso limite di ellisse in quanto se l'eccentricità è zero la direttrice deve allontanarsi all'infinito.
Si può dunque affermare che l'eccentricità di una sezione conica dia una misura di quanto essa si allontani dall'essere circolare.
Per una data lunghezza del semiasse maggiore, quanto più si avvicina a 1, tanto più piccolo è il semiasse minore
consistente in tutti i punti la cui distanza da F è uguale al prodotto di e per la rispettiva distanza da d.
La circonferenza è il luogo geometrico dei punti equidistanti dal centro.
Per determinare l'equazione della circonferenza imponiamo quindi che la distanza del punto generico P(x,y) dal centro C(x0,y0) sia uguale al raggio r.
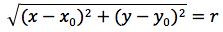
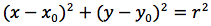
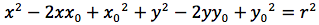
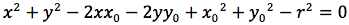
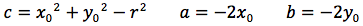
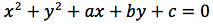
Affinché un'equazione di secondo grado a due incognite, rappresenti una circonferenza, è necessario e sufficiente quindi, che non ci sia il termine in xy, che i coefficienti di x2 e y2 siano uguali ed infine che x02+y02-c sia un valore positivo.
L'ellisse e' il luogo geometrico dei punti del piano per cui e' costante la somma delle distanze da due punti fissi detti fuochi
Per tutti i punti P della figura avremo che d(P;F1)+d(P;F2)=costante.
Per sapere quanto vale la costante spostiamo il punto P fino a portarlo sull'asse orizzontale, allora si vede che la somma d(P;F1)+d(P;F2) e' uguale alla distanza fra i due punti dell'ellisse che tagliano l'asse delle x (asse orizzontale). Chiamiamo questa distanza 2a (a per indicare che e' una costante e 2 perche', essendo l'ellisse simmetrica spesso ci servira' la meta' della distanza, cioe' il semiasse orizzontale); quindi avremo per tutte le ellissi d(P;F1) + d(P;F2) = 2a con a semiasse orizzontale. I due fuochi abbiano coordinate (-c,0) (c,0). Passando a calcolare l'equazione dell'ellisse con asse corrispondente all'asse delle ascisse avremo:
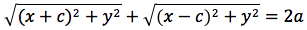
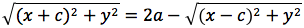
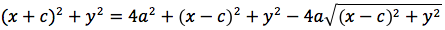
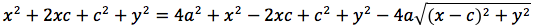
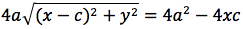
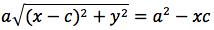
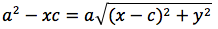
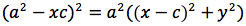
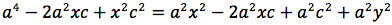
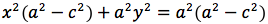
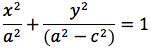
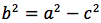
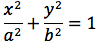
L'ellisse possiede interessanti proprietà di carattere ottico. Infatti, supponiamo di avere un riflettore di forma ellittica. Se si pone una sorgente di luce in uno dei due fuochi, tutti i raggi riflessi passano per l'altro fuoco. Questo ci da inoltre, una spiegazione dei nomi dati a tali punti F, F'. Supponiamo adesso di essere in un ambiente di forma ellittica. Il suono emesso in uno dei due fuochi, anche se molto debole, si sente molto distintamente nell'altro fuoco. Infatti in entrambi i casi, sia le onde luminose che sonore, che sono riflesse dalle pareti percorrono tutte la stessa distanza e giungono contemporaneamente (in fase) all'altro fuoco.
La parabola è il luogo dei punti del piano le cui distanze da un punto chiamato fuoco e da una retta chiamata direttrice sono uguali.
Determiniamo l'equazione di una parabola avente per direttrice una retta orizzontale di equazione y=d e per fuoco il punto F di coordinate (x0,y0). In figura si noti che la direttrice non corrisponde all'asse delle ascisse e che il fuoco non può appartenere alla direttrice. Indichiamo con P(x,y) un punto generico della parabola e imponiamo che la distanza punto fuoco d(P,F) sia uguale alla distanza punto direttrice. Il punto H giacendo sulla stessa verticale deve avere identica ascissa di P quindi H(x,d). Imponiamo quindi la condizione d(P,F)=d(P,H), siccome
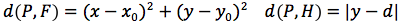
uguagliando d(P;F) e d(P,H) otteniamo
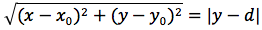
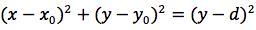
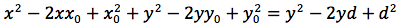
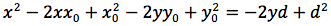
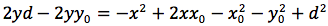
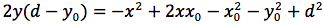
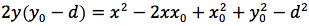
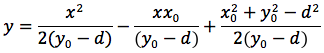
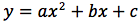
L'iperbole e' il luogo geometrico dei punti del piano per cui e' costante la differenza delle distanze da due punti fissi detti fuochi
Significa che per tutti i punti P della figura avremo che PF2 - PF1 = costante.
Per sapere quanto vale la costante spostiamo il punto P fino a portarlo sull'asse orizzontale, allora si vede che la differenza d(P;F1)-d(P;F2) e' uguale alla distanza fra i due punti dell'iperbole che tagliano l'asse delle x (asse orizzontale).
Chiamiamo questa distanza 2a (a per indicare che e' una costante e 2 perche', essendo l'iperbole simmetrica spesso ci servira' la meta' della distanza, cioe' il semiasse orizzontale); quindi avremo per tutte le iperboli d(P;F1)+d(P;F2)=costante=2a con a semiasse orizzontale. I due fuochi abbiano coordinate (-c,0) (c,0). Eseguendo i calcoli determiniamo l'equazione dell'iperbole con asse corrispondente all'asse delle ascisse:
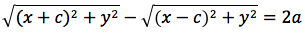
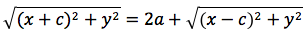
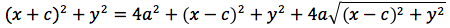
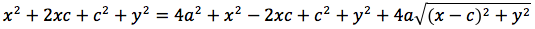
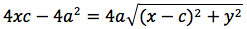
dividendo per 4 si ottiene:
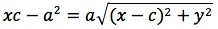
si quadra:
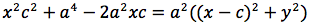
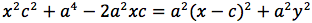
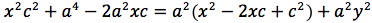
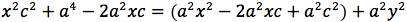
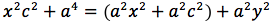
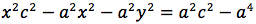
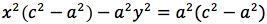
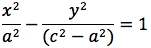
ponendo
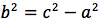
si ottiene infine:
