Definizione: dati due insiemi non vuoti A e B chiamati rispettivamente dominio e codominio, si chiama relazione di A in B una legge che associa ad elementi di A, elementi di B.
Definizione: dati due insiemi non vuoti A e B chiamati rispettivamente dominio e codominio, si chiama funzione o applicazione di A in B, una relazione che associa ad ogni elemento di A, uno ed uno solo di B.
La funzione si indicherà f:A→B. Si dice che f è definita in A con valori in B. La x che denota il generico elemento di A si chiama la variabile. f(x) si dice immagine di x tramite la f.
Definizione: Il sottoinsieme del codominio costituito da gli elementi che sono i corrispondenti di qualche elemento del dominio si chiama insieme immagine della f.
L'insieme immagine della f si indicherà con f(A). Si noti che un elemento di B può anche non essere immagine di alcun elemento di A. Si noti ancora che un elemento di B può essere il corrispondente di più di un elemento di A.
Definizione: Dati due insiemi non vuoti A e B si dice prodotto cartesiano tra A e B, l'insieme delle coppie ordinate di cui il primo elemento appartiene ad A ed il cui secondo a B.
Il numero di coppie dell'insieme AxB è uguale al prodotto del numero degli elementi di A per il numero degli elementi di B.
Definizione: Il sottoinsieme del prodotto cartesiano AxB costituito da quelle coppie i cui elementi si corrispondono, tramite la funzione, si chiama grafico di f.
Il grafico di una funzione f lo indicheremo con G(f).
Definizione: La funzione f si dice suriettiva se f(A)=B.
Per formare applicazioni suriettive tra insiemi finiti, il numero di elementi del dominio dev'essere maggiore o uguale del numero di elementi del codominio.
Definizione: la funzione f si dice iniettiva se ogni elemento dell'insieme immagine proviene da un'unico elemento del dominio, ovvero da x≠y ne consegue che f(x)≠f(y).
Per formare applicazioni iniettive tra insiemi finiti, il numero di elementi del dominio dev'essere minore o uguale del numero di elementi del codominio.
Definizione: La funzione f si dice biettiva se risulta contemporaneamente sia iniettiva che suriettiva.
Per formare applicazioni biettive tra insiemi finiti, il numero di elementi del dominio dev'essere uguale del numero di elementi del codominio.
Definizione: La funzione f si dice costante se l'insieme immagine è costituito da un solo elemento.
Di seguito sono rappresentati i diagrammi sagittali e cartesiani, di alcune relazioni tra insiemi che contengono un numero finito di elementi.
Esempio 1
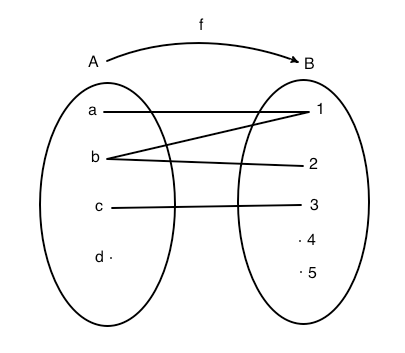
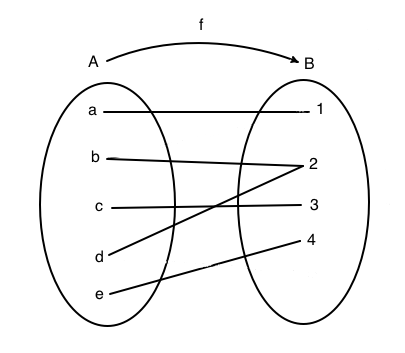
Ci sono due motivi per cui la relazione in figura non è una funzione. Nel diagramma sagittale a sinistra, lo si nota dal fatto che l'elemento b del dominio corrisponde a due elementi dell'insieme immagine cioè 1 e 2. Il secondo motivo è che l'elemento d non ha alcun corrispondente nell'insieme immagine. La definizione di funzione non è soddisfatta quindi si tratta di una semplice relazione. Nel diagramma cartesiano, a destra, il fatto che a b corrispondono i due valori 1 e 2 lo si nota perchè sulla verticale conotta da b ci sono due punti, inoltre, siccome sulla verticale condotta da d non si trova alcun punto si nota che d stesso non corrisponde ad alcun elemento dell'insieme immagine. Una relazione è funzione quando nel relativo diagramma cartesiano, su ogni verticale condotta dagli elementi del dominio c'è un'unico punto.
Esempio 2
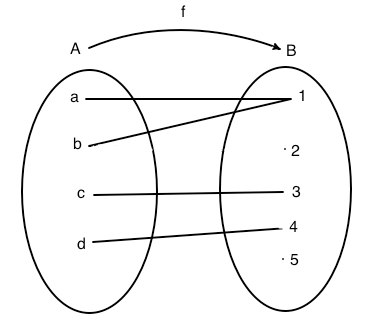

In figura è rappresenta una funzione senza particolari proprietà. L'insieme immagine è il sottoinsieme di B f(A)={1, 3, 4}. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,1), (c,3),( d,4)}. Nel diagramma cartesiano si nota che 2 e 5 non appartengono all'insieme immagine poichè sulle orizzontali condotte da questi due valori non c'è alcun punto.
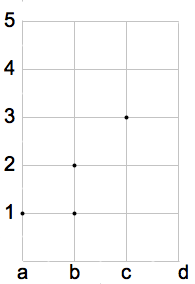
Esempio 3
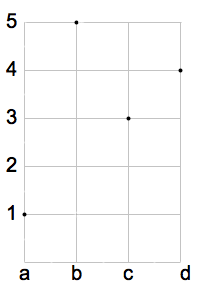
In figura è rappresenta una funzione iniettiva. Nel diagramma cartesiano si nota che su ogni orizzontale condotta dagli elementi del codominio c'è al massimo un punto. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,5), (c,3),( d,4)}.
Esempio 4
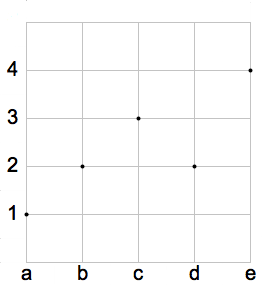
In figura è rappresenta una funzione suriettiva. Nel diagramma cartesiano si nota che su ogni orizzontale condotta dagli elementi del codominio c'è almeno un punto. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,2), (c,3),( d,2), (e,4)}.
Esempio 5
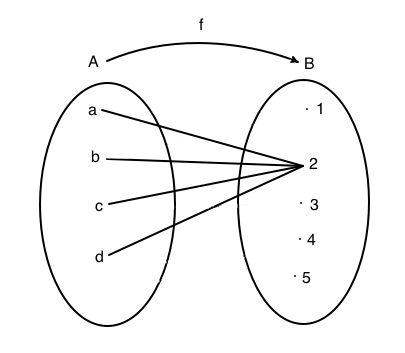
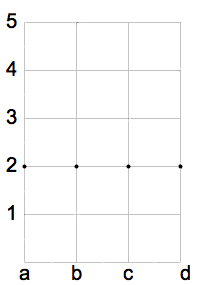
In figura è rappresenta una funzione costante. Nel diagramma cartesiano si nota che tutti i valori dell'insieme immagine stanno sulla stessa orizzontale. Il grafico della funzione è costituito dall'insieme: G(f)={(a,2), (b,2), (c,2),( d,2)}.
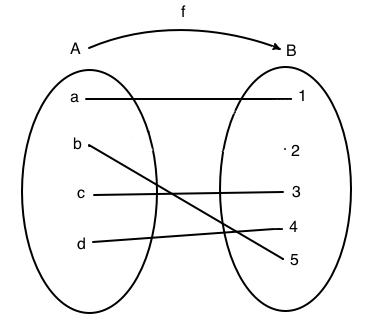
Esempio 6
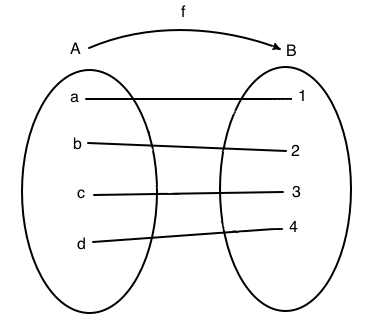
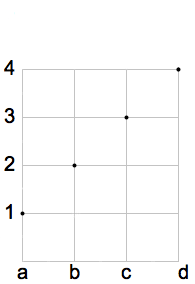
In figura è rappresenta una funzione biettiva. Nel diagramma cartesiano si nota che su ogni orizzontale c'è un unico punto. Il grafico della funzione è costituito dall'insieme: G(f)={(a,1), (b,2), (c,3),( d,4)}.
Nell'esempio presentato nella figura di sotto c'è una funzione h che ha valori in B ed una funzione g che assume valori in C, nell'ipotesi che l'insieme immagine della h sia contenuto nel dominio g si può considerare la funzione f che ha dominio in A e assume valori in C, ottenuta applicando in successione la funzione h e poi la funzione g.
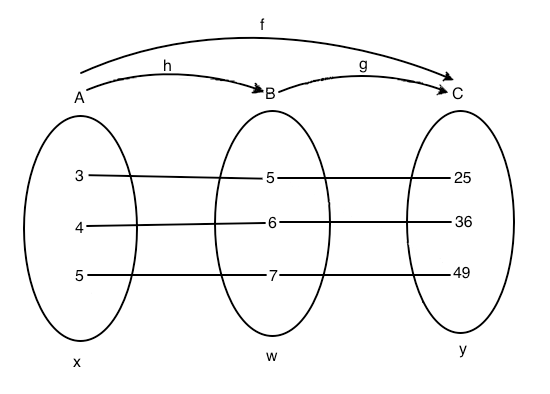
La funzione f così ottenuta si chiama funzione composta.
La funzione composta può essere scritta in due modi diversi: f(x) = g(h(x)) oppure f(x) = (goh)(x). Si noti che nella notazione della funzione composta (goh)(x) è scritta prima la g e poi la h anche se prima si applica la h e poi la g.
In figura ci sono tre funzioni:
h: A→ B w = h(x) = x+2
g: B→ C y = g(w) = w2
f: A→ C y = f(x) = g(h(x)) = (goh)(x) = (x+2)2
La funzione h espressa a parole sarebbe "aggiungi 2", la g sarebbe "esegui il quadrato".
La funzione f è la composta di h con g.
L'operazione di composizione non gode della proprietà commutativa. Per dimostrare ciò basta trovare un controesempio. E' sufficiente quello presentato in figura, se si considera la h(g(x)) allora al numero 3 attraverso la g corrisponde il 9 ed al numero 9 attraverso la h corrisponde il numero 11, quindi h(g(3))=11 mentre g(h(3))=25, la funzione (hog)(x) infatti, ha la seguente espressione analitica y=x2+2 che non corrisponde con la (goh)(x)=(x+2)2.
Problema diretto dato un insieme A di numeri si vuol costruire una funzione che li elevi al quadrato e quindi tolga tre. y=f(x)=x2-3 Problema inverso dato un insieme B di numeri si vuol costruire una funzione che aumenti i numeri di tre e quindi calcoli la radice. x=g(y)=√(x+3) Più in generale, per risolvere un certo problema, potrebbe essere importante saper individuare la funzione inversa cioè una funzione ottenuta scambiando dominio con codominio e che faccia corrispondere gli stessi elementi della funzione diretta. Da tener presente che se una funzione non è biettiva, l'inversa non è una funzione, ma una semplice relazione. Dunque le uniche funzioni invertibili sono quelle biettive.
La funzione inversa della f si indica con f-1
Attenzione a non confondere questa notazione con quella della funzione reciproca 1/f
Se una funzione non è biettiva la si rende tale con delle opportune restrizioni che possono coinvolgere tanto il dominio che il codominio, ciò significa che si determina un sottoinsieme A' di A e un sottoinsieme B' di B tali che la f: A → B sia biettiva in tal modo si può considerare la f-1: B' → A'
Una funzione f: A → B è l'inversa una funzione g: B → A se
g(f(x)) = x ∀ x ∈ A, e
f(g(y)) = y ∀ y ∈ B;
(gοf)(x) = i(x) dove con i(x) si è indicata la funzione identica
(fοg)(y)=i(y) dove con i(y) si è indicata la funzione identica
Invertibilità della funzione lineare

Data la funzione lineare y=f(x)=2x+1 f: Q → Q cerchiamo di individuare la relativa inversa. Per prima cosa ci si pone il problema di valutare se la funzione stessa è invertibile. La funzione lineare presa in esame, è biettiva, lo si nota poichè su ogni orizzontale c'è sempre solo un punto della funzione stessa. Essendo biettiva è invertibile, senza dover eseguire alcuna restrizione. La funzione inversa f-1: R → R, ha quindi ancora l'insime Q per dominio e codominio. Per individuare l'espressione analitica dell'inversa dobbiamo esplicitare la variabile x ovvero -2x=-y+1 e dividendo per -2 si ottiene x=f-1(y)=(y-1)/2. A questo punto per poter porre sullo stesso sistema di riferimento sia la f che la f-1 rinominiamo le variabili ovvero y=f-1(x)=(x-1)/2. Notiamo che la f espressa a parole è: "moltiplica per 2 e somma 1". La f-1 invece: "sottrai 1 e dividi il risultato per due". Si noti che per esprimere la f-1 a parole basterebbe leggere da destra verso sinistra la f eseguendo però le operazioni inverse. In figura si noti che f e f-1 sono simmetriche rispetto alla retta y=x questo perchè per disegnare la funzione inversa si sono dovuti ruotare gli assi cartesiani, sempre sulla retta y=x in modo da invertire l'asse delle x con quello delle y.
Invertibilità della funzione y=x2

Data la funzione y=f(x)=x2 f: R → R cerchiamo di individuare la relativa inversa. Per prima cosa ci si pone il problema di valutare se la funzione stessa è invertibile.
La funzione presa in esame, non è biettiva, lo si nota poichè sulle orizzontali condotte sopra lo zero ci sono sempre due punti di intersezione con la funzione stessa, mentre sulle orizzontali condotte sotto lo zero non ci sono punti di intersezione con la funzione stessa.
Non essendo quindi la funzione nè suriettiva nè iniettiva bisogna restringere sia il dominio che il codominio.
Per rendere la funzione iniettiva si deve restringere il dominio a R0+, in tal modo , infatti su ogni orizzontale ci sarà al massimo un solo punto di intersezione con la funzione. Per renderla anche suriettiva si deve restringere anche il codominio a R0+, in tal modo , infatti su ogni orizzontale ci sarà al massimo un solo punto di intersezione con la funzione.

Per individuare l'espressione analitica dell'inversa dobbiamo esplicitare la variabile x ovvero x=√y.
A questo punto per poter porre sullo stesso sistema di riferimento sia la f che la f-1 rinominiamo le variabili ovvero y=f-1(x)=√x. Nella figura di fianco notiamo che f e f-1 sono simmetriche rispetto alla retta y=x questo perchè per disegnare la funzione inversa si sono dovuti ruotare gli assi cartesiani, sempre sulla retta y=x in modo da invertire l'asse delle x con quello delle y. Si noti ancora che y=√x e y=x2 hanno due punti di contatto ovvero l'origine e il punto (1;1) infatti 02=√0 e 12=√1. Prestiamo attenzione ancora al fatto che sarebbe sbagliato dire che √9=3 o anche √9=-3 perchè in questo caso a 9 corrisponderebbero due valori e quindi y=√x non sarebbe una funzione. Ovviamente a √9 è associato l'unico valore 3.
Siano f(x) e g(x) due funzioni aventi uno stesso dominio A, se ciò non succede si assume A come intersezione dei domini di f e g. Ci si chiede se esistono dei valori appartenenti ad A per i quali le due funzioni risultano uguali, ovvero supponendo che le due funzioni siano espresse attrverso una rappresentazione analitica bisogna valutare se esistono dei valori appartenenti ad A tali che f(x)=g(x). Quella che abbiamo scritto è un'equazione con incognita x ed un valore s tale che f(s)=g(s) si chiama soluzione dell'equazione.
La funzione esponenziale f(x)=bx pensata come funzione f: R → R è una funzione iniettiva ma non suriettiva, lo si nota dai relativi grafici poichè le orizzontali del tipo y=p con p numero positivo hanno un'intersezione con il grafico della funzione invece le orizzontali del tipo y=n con n negativo non hanno intersezione come non ha intersezioni l'asse x stessa. Per rendere la funzione biettiva e quindi invertibile si dovrà restringere il codominio all'insieme immagine ovvero R+. Si studiano due casi di funzioni esponenziali a seconda che la base assuma un valore compreso tra zero e uno oppure un valore maggiore di uno. Non ha interesse il caso in cui la base b sia uguale a zero poichè y=0x corrisponde all'asse delle x e non ha interesse il caso in cui la base b sia uguale a uno poichè y=1x corrisponde alla retta orizzontale y=1. Non si studia, e non avrebbe senso farlo, studiare la funzione esponenziale con la base negativa.
L'introduzione dei numeri relativi è dovuta al fatto che nell'insieme dei numeri naturali manca l'opposto. L'introduzione dei numeri razionali è dovuta al fatto che nell'insieme dei numeri relativi manca il reciproco. Se l'estensione N→Z e Z→Q sono motivate quindi da esigenze di carattere algebrico, diverso è il carattere dell'estensione Z→R. Consideriamo un problema geometrico. La retta non viene definita direttamente, ma le sue proprietà risultano dai postulati, che noi possiamo ammettere, decidendo come vogliamo pensare sia fatta la retta. Se, per esempio costruiamo, a partire dall'origine, un quadrato di lato 1, ci si chiede il cerchio che ha per raggio la diagonale del quadrato, taglierà da qualche parte la retta. Non c'è dubbio che, andando dietro alla nostra intuizione, la risposta alla domanda sarà certamente "si".
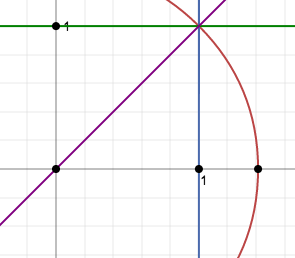
Infatti la diagonale del quadrato è √2, ma pensando che √2 non è un numero razionale, si deve ammettere che i punti di ascissa razionale non esauriscono la retta altrimenti dobbiamo ammettere che la retta stessa abbia un buco in √2. A tal proposito si può dimostrare facilmente che x2=2 non ha soluzioni nel campo dei numeri razionali. Quindi, bisogna supporre l'esistenza di nuovi enti e definirli, partendo dai numeri razionali e ritrovare, tra questi i numeri razionali stessi. Se nell'esempio precedente, la circonferenza non intersecasse la retta, l'insieme dei punti della retta potrebbe essere ripartito in due classi. La prima classe conterrebbe i punti S a sinistra dello zero e quei punti S a destra dello zero tali che OS2<2OU2 con OU a rappresentare il segmento [0;1]. La seconda classe conterrebbe i punti D a destra dello zero tali che OD2>2OU2 con OU a rappresentare il segmento [0;1]. Ogni punto della retta troverebbe posto in una (e una sola) delle due classi, la prima sarebbe priva di massimo e la seconda sarebbe priva di minimo. Un numero reale sarà pensato come originato da una coppia di semirette razionali.
Ci sono diversi modi di introdurre i numeri reali: quello delle coppie di classi contigue (Cantor), quello delle coppie di successioni convergenti, qui faremo riferimento a quello delle sezioni del campo razionale (Dedekind).
Diremo sezioni del campo razionale ogni coppia (S,D) di classi di numeri razionali che soddisfa le segurnti condizioni:
Si distingueranno le sezioni di prima specie, quelle in cui c'è un numero razionale escluso da entrambe le classi e sezioni di seconda specie, quelle per le quali è S∪D=Q
Definizione: un numero reale è ogni sezione del campo razionale. L'insieme dei numeri reali si indicherà con R.
Con R+0 indicheremo l'insieme dei numeri reali positivi compreso lo zero
Con R-0 indicheremo l'insieme dei numeri reali negativi compreso lo zero
Con R+ indicheremo l'insieme dei numeri reali positivi escluso lo zero
Con R- indicheremo l'insieme dei numeri reali negativi escluso lo zero
Si vuole ora estendere la definizione di potenza al caso di esponente reale.
Per esempio √2 sarà rappresentato dalla sezione (S , D) con S = {Q- ∪ x∈Q+: x2<2} e D = {x∈Q+: x2>2}. All'insieme S appartengono numeri razionali come 1 , 1.4, 1.41, 1.414, … e all'insieme D appartengono numeri razionali come 2 , 1.5, 1.42, 1.415, … Si tratta di una sezione di seconda specie. Dato b > 0 supponiamo di associare alle classi S , D dell’esempio le classi: H={h∈Q: h=bx x∈S}, K={k∈Q: k=bx x∈D}. All'insieme H appartengono numeri razionali come b 1, b 1.4, b 1.41, b 1.414, … All'insieme K appartengono numeri razionali come b 2, b 1.5, b 1.42, b 1.415, … Allora è naturale pensare che a√2 sarà rappresentato dalla sezione ( H , K ). Si dà allora la seguente definizione:Definizione: si definisce potenza del numero reale positivo a con esponente reale w il numero reale positivo aw definito dalla sezione costituite dalle potenze di a che hanno per esponenti i numeri appartenenti alle due classi che definiscono l’esponente k.
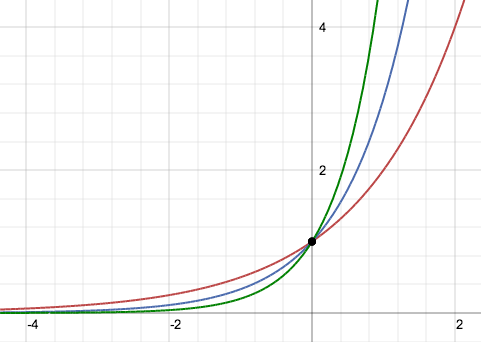
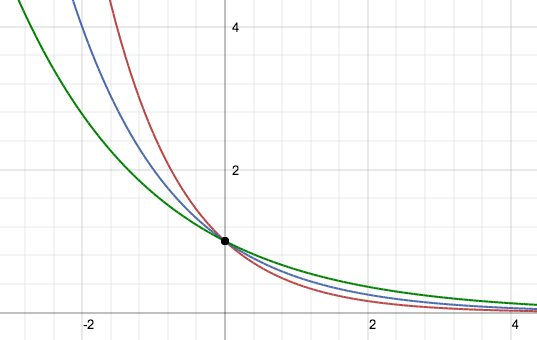
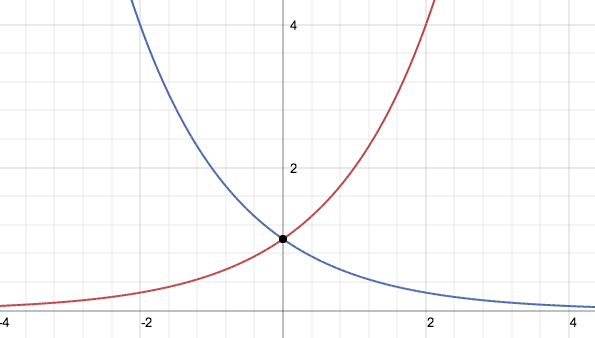
Un'equazione è da considerarsi esponenziale se presenta almeno una potenza che abbia l'incognita nel proprio esponente.
Le equazioni esponenziali possono presentarsi sotto diverse forme per cui non esiste un metodo generale per la loro risoluzione, si daranno alcune indicazioni di carattere generale e si analizzeranno solamente dei casi particolari.
L'equazione esponenziale più semplice che possiamo scrivere è la seguente: bx=a con b>0. Valutiamo che cosa può succedere in questo caso
Se l'equazione proposta è del tipo bx=a con a<0 allora l'quazione è impossibile poichè bx è sempre positivo per qualsiasi valore attrbuito alla variabile x.
Se l'equazione proposta è del tipo 1x=a con a diverso da uno allora l'equazione è impossibile poichè 1x è sempre uguale a uno per qualsiasi valore attribuito alla variabile x.
L'equazione 1x=1 è indeterminata in quanto è soddisfatta per ogni valore attribuito alla variabile x.
Se a e b sono positivi e si riescono a scrivere come potenze della stessa base allora l'equazione sara determinata e potrà essere risolta con semplici passaggi per esempio: 9x=81 → 32x=34 da cui, siccome le basi sono uguali possiamo scrivere che gli esponenti sono uguali: 2x=4 → x=2.
Applicando il logaritmo e le sue proprietà si possono risolvere quindi equazioni esponenziali che non presentano basi uguali. Per la risoluzione di altri casi particolari di funzioni esponenziali si rimanda alla parte esercizi.
La funzione logaritmica è l'inversa della funzione esponenziale. La funzione esponenziale è invertibile se si restringe il codominio a R+. La funzione logaritmo, quindi ha per dominio R+. Non ha senso quindi, calcolare il valore di un logaritmo che ha per argomento un numero negativo.
Dato un numero positivo a, che chiameremo argomento e un numero b che chiameremo base, il logaritmo in base b di a, è l'esponente che bisogna assegnare alla base per ottenere l'argomento.
Dalla definizione ne consegue quindi che logba=x se e solo se bx=a. Si studiano due casi di funzioni logaritmiche, a seconda che la base assuma un valore compreso tra zero e uno oppure un valore maggiore di uno.
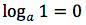
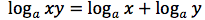
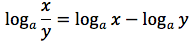
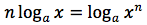
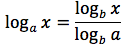
Dimostrazione della prima proprietà
Il logaritmo di uno, in una qualsiasi base, è uguale a zero poichè a0=1.
Dimostrazione della seconda proprietà
si ponga:
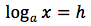
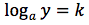
In tal modo per definizione avremo:
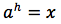
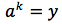
Da cui per le proprietà delle potenze e per definizione di logaritmo:
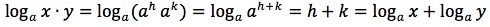
Dimostrazione della terza proprietà
si ponga:
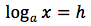
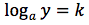
In tal modo per definizione si ha:
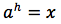
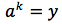
Da cui per le proprietà delle potenze e per definizione di logaritmo:
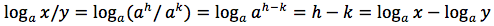
Dimostrazione della quarta proprietà
si ponga:
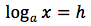
in tal modo si ha:
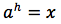
elevando entrambi i membri alla n si ha:
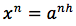
Da cui:
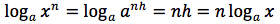
Dimostrazione della quinta proprietà
si ponga:
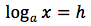
In tal modo per definizione avremo:
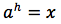
Applicando ad entrambi i termini dell'uguaglianza il logaritmo in base b si ottiene ancora un'uguaglianza:
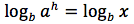
Per la quarta proprietà l'esponente h diventa un fattore per cui si ottiene:
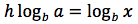
Ricavando h come fosse l'incognita di un'equazione si ottiene:
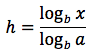
Dato che h è uguale a logaritmo in base a di x, sostituendo si ottiene:
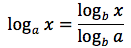
Questa proprietà può essere utile per un cambiamento di base nel calcolo del logaritmo.



Un'equazione è da considerarsi logaritmica se presenta almeno un logaritmo che abbia l'incognita nel proprio argomento.
Consideriamo equazioni logaritmiche che possano essere scritte nella seguente forma:
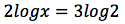
Per la risoluzione di un'equazione logaritmica si procederà per gradi:
Se l'equazione proposta non è del tipo previsto tentare, qualora fosse possibile di trasformarla applicando le proprietà del logaritmo.
Determinare il campo di esistenza delle soluzioni risolvendo il sistema comprendente la disequazioni f(x)>0, g(x)>0 in quanto l'argomento del logaritmo dev'essere strettamente maggiore dello zero.
Cercare le soluzioni dell'equazione f(x)=g(x) dove con f(x) e g(x) indichiamo due funzioni della variabile x.
Si può anche, senza calcolare il campo di esistenza delle soluzioni, risolvere l'equazione f(x)=g(x) e quindi verificare che le stesse rendano l'argomento del logaritmo maggiore di zero. Un valore, soluzione dell'equazione f(x)=g(x) che non soddisfi a questa condizione non può essere acettato come soluzione dell'equazione logaritmica
Le funzioni goniometriche sono funzioni che associano angoli a numeri reali, sono quindi funzioni che hanno angoli nel dominio e numeri reali nel codominio.
Le unità di misura più usate per misurare gli angoli sono due: il grado ed il radiante.
Definizione: il grado è la trecentosessantesima parte dell'angolo giro.
Definizione: il radiante è l'angolo al centro di una circonferenza che "sottende" un arco di lunghezza uguale al raggio.
Il sistema di misurazione in cui l'unità è il grado è chiamato sistema sessagesimale in quanto il sottomultiplo del grado è il primo che è la sessantesima parte del grado e il sottomultiplo del primo è il secondo che è la sessantesima parte del primo.
Il grado viene usato più frequentemente nei calcoli. Il radiante viene usato soprattutto, per disegnare i grafici delle funzioni goniometriche. La definizione di grado deriva storicamente dal fatto che, pensando la terra ferma al centro dell'universo, il sole ne fa un giro completo in circa 360 giorni. I sottomultipli del grado, primi e secondi, stanno come i minuti ed i secondi rispetto all'ora. La definizione di radiante sfrutta il fatto che tra circonferenza e raggio c'è il rapporto costante 2π.
Per passare attraverso i calcoli da un'unità di misura all'altra bisogna vanno impostate delle proporzioni. Si sfrutta per esempio il fatto che un angolo giro è 180 gradi che corrisponde π radianti. Se vogliamo sapere quanto misura in gradi un radiante, impostiamo la seguente proporzione: x°:1=180:π da cui segue: x°=180/π otteniamo 57,295779, ma le cifre dopo la virgola esprimono i sottomultipli del grado in decimi, centesimi, millesimi.... sappiamo invece che i sottomultipli del grado sono espressi in primi e secondi che sono rispettivamente la sessantesima parte del grado e la sessantesima parte del primo. E' necessario quindi convertire il numero 0,295779 in sessantesimi, va impostata quindi una nuova proporzione: 295779:1000000=x:60 da cui x=(60*295779)/1000000=17,746770. La parte intera del numero così trovato cioè 17 rappresenta i primi, la parte del numero 0,746770, dopo la virgola analogamente va convertita in sessantesimi quindi si imposta la nuova proporzione 746770:1000000=x:60 da cui si ottiene 44,9 che rappresenta il numero dei secondi quindi arrotondando dunque si ottiene:
1 rad=57° 17' 45''.
Dovendo convertire i gradi in radianti per esmpio se vogliamo sapere quanto misura in radianti un grado, impostiamo la seguente proporzione: 1:xrad=180:π da cui x=π/180=0,01745, per cui si ottiene:
1°= 0,01745rad
Analogamente si procede per trasformare la misura di un qualsiasi angolo da un'unità di misura all'altra. Con la calcolatrice scientifica queste operazioni si eseguono comunque in modo automatico.
Definizione: Chiameremo circonferenza goniometrica la circonferenza avente centro nell'origine del sistema di riferimento e raggio di lunghezza 1.
In figura è rappresentata la circonferenza goniometrica. Sia P un punto vincolato a percorrere la circonferenza in senso antiorario. Sia x l'angolo al centro della circonferenza AOP.
Definizione: sin(x)=PH
Definizione: cos(x)=OH
Definizione: tan(x)=AT
Definizione: cot(x)=EC
Si sono volute indicare le funzioni seno, coseno, tangente e cotangente con i simboli sin cos tan e cot che sono i simboli con cui queste funzioni vengono individuate dalle calcolatrici scientifiche. Il punto P quindi ha per ascissa cosx e per ordinata sinx. Il seno ed il coseno assumono quindi valori che vanno da -1 a 1, la tangente e la cotangente invece, assumono valori tra +∞ e -∞.

Calcoliamo il seno di 30° ovvero di π/6 rad.
A destra, in figura, supponiamo che l'angolo CAB sia di 30° supponiamo anche che AC sia uguale al raggio della circonferenza goniometrica ovvero 1. Se facciamo compiere al triangolo ABC una rotazione attorno al lato AB otteniamo il triangolo ABC'. Tale triangolo è equiangolo e quindi equilatero, infatti l'angolo ACB è 60° come pure l'angolo BC'A in quanto è ottenuto raddoppiando un angolo di 30° ed anche BC'A è 60°. In tale triangolo la bisettrice AB è pure altezza ma anche mediana per cui divide il lato CC'in due parti uguali. Il lato CC' è 1 perchè si tratta di un triangolo equilatero, BC è quindi 1/2 e questo valore corrisponde proprio al seno di 30°.
Calcoliamo ora il seno di 45° ovvero π/4 rad.
A destra, in figura, l'angolo DFG è 45° allora anche l'angolo FDG è 45°, Infatti l'angolo DFG è retto per costruzione e siccome la somma degli angoli interni di un triangolo è 180° allora gli altri due angoli sono anch'essi di 45°. Da queste considerazioni ne consegue che il triangolo DFG è isoscele. Il seno di 45° é quindi uguale al coseno di 45° e per calcolare questo valore sfruttiamo il teorema di Pitagora. Chiamato x il seno ed il coseno di 30° possiamo impostare la seguente equazione:
x2+x2=1 ovvero 2x2=1 ovvero x2=1/2 ovvero x= √(1/2) e razionalizzando il denominatore x=(√2)/2.
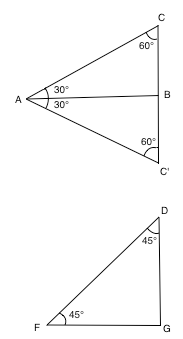
Notiamo che sen30°=cos60°, ma più in generale che sin(α)=cos(90°-α). Per calcolare i valori di tangente e cotangente sarà sufficiente pensare che tanx=sinx/cosx quindi tan30°=√3/3, tan45°=1, tan60°=√3.
Per angoli associati si intendono i seguenti angoli: 90°-α, 90°+α, 180°-α, 180°+α 270°-α, 270°+α , 360°-α.
A destra in figura, l'angolo AOB sia α e l'angolo BOC sia 180°-α.
Si può notare che CD=BA, ma
CD=sin(180°-α)
BA=sin(α),
da cui:
sin(180°-α)=sin(α)
analogamente DO=-OA ovvero:
cos(180°-α)=-cos(α)
Accanto a quelle già scritte si possono ricavare ulteriori relazioni tra i valori che le funzioni assumono negli angoli associati:
sin(180°-α)=sin(α) sin(180°+α)=-sin(α) sin(360°-α)=-sin(α).
cos(180°-α)=-cos(α) cos(180°+α)=-cos(α) cos(360°-α)=cos(α)

A destra in figura, l'angolo AOB sia α e l'angolo DOA sia 180°-α.
Si può notare che AB=-BC
AB=tan(α)
BC=tan(180-α)
da cui:
tan(α)=-tan(180-α)
Accanto a quelle già scritte si possono ricavare ulteriori relazioni tra i valori che le funzioni assumono negli angoli associati:
tan(180°-α)=-tan(α) tan(180°+α)=tan(α) tan(360°-α)=-tan(α)
cot(180°-α)=-cot(α) cot(180°+α)=cot(α) cot(360°-α)=-cot(α).

A destra, in figura, consideriamo il primo quadrante della circonferenza goniometrica. L'angolo AOB, che in figura è chiamato angolo α, lo si è costruito uguale all'angolo EOC, l'angolo COD è quindi 90°-α.
Il lato AB è sin(α) e il lato CD è cos(90°-α).
I due triangoli OAB e COD sono uguali per avere un lato uguale e due angoli uguali.
I lati sono OC=OA (perchè entrambi sono il raggio della circonferenza goniometrica).
I due angoli uguali sono rispettivamente CDO=ABO=90° e AOB=OCD=α, per costruzione.
Gli elementi dei due triangoli sono quindi uguali, in particolare OD=AB in quanto lati opposti ad angoli uguali in triangoli uguali, ma OD=cos(90°-α) e AB=sin(α) quindi vale la seguente relazione:
sin(α)=cos(90°-α)
Accanto a quella scritta si possono ricavare ulteriori relazioni tra i valori che le funzioni assumono negli angoli associati:
sin(α)=-cos(90+α) sin(90°-α)=cos(α)
sin(90°+α)=cos(α) cos(α)=-sin(270°+α)
cos(270°+α)=sin(α) sin(α)=-cos(270°-α)
sin(270°-α)=-cos(α)
La tabella, a destra, comprende alcuni valori delle funzioni seno, coseno, tangente, cotangente, ottenuti con le relazioni sugli angoli associati e tenendo conto dei valori che queste funzioni assumono quando l'angolo α è di 30°, 45°, 60°.
La funzione seno nel primo e secondo quadrante assume valori positivi, nel terzo e quarto valori negativi.
La funzione coseno nel primo e quarto quadrante assume valori positivi, nel secondo e terzo valori negativi.
La funzione tangente nel primo e terzo quadrante assume valori positivi, nel secondo e quarto valori negativi.
La funzione cotangente nel primo e terzo quadrante assume valori positivi, nel secondo e quarto valori negativi.
La funzione tangente è data dal rapporto sinx/cosx, per cui a 90°, 270° non esiste in quanto cos90°=cos270°=0, analogamente la funzione cotangente è data dal rapporto cosx/sinx, per cui a 0°, 180° non esiste in quanto sen0°=sin180°=0. Se l'angolo α da 0° tende a diventare un angolo retto, la funzione tanα tende a +∞. Se l'angolo α da 120° tenden a diventare un angolo retto, la funzione tanα tende a -∞. Se l'angolo α da 120° tende a diventare un angolo di 270°, la funzione tanα tende a +∞. Se l'angolo α da 0° tende a diventare un angolo di 270°, la funzione tanα tende a -∞

| x° | xrad | sen(x) | cos(x) | tan(x) | cot(x) |
| 0 | 2π | 0 | 1 | 0 | 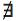 |
| 30 | π/6 | 1/2 | √3/2 | √3/3 | √3 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60 | π/3 | √3/2 | 1/2 | √3 | √3/3 |
| 90 | π/2 | 1 | 0 | 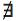 | 0 |
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 |
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | tan(x) |
| 180 | π | 0 | -1 | 0 | 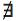 |
| 210 | 4π/3 | -1/2 | -√3/2 | √3/3 | √3 |
| 225 | 5π/4 | -√2/2 | -√2/2 | 1 | 1 |
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 |
| 270 | 3π/2 | 1 | 0 | 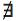 | 0 |
| 300 | 5π/3 | -√3/2 | 1/2 | -√3 | -√3/3 |
| 315 | 7π/4 | -√2/2 | √2/2 | -1 | -1 |
| 330 | 11π/6 | -1/2 | √3/2 | -√3/3 | -√3/3 |
| 360 | 2π | 0 | 1 | 0 | 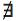 |

In figura il grafico della funzione sinx l'unità di misura degli angoli è il radiante. L'insieme immagine della funzione seno è l'intervallo compreso tra -1 e 1. E' una funzione periodica di periodo 2π. Si può dimostrare che il grafico della funzione seno ha delle specifiche caratteristiche sempre nel caso in cui l'unità di misura sia il radiante e la scala 1:1. In particolare la tangente nell'origine alla funzione corrisponde alla retta y=x. Si veda Limiti notevoli. Per questo motivo nella rappresentazione della funzione si usa tale unità di misura. Se usassimo il grado il grafico della funzione seno sarebbe sempre una sinusoide ma molto più "allungata" per eseguire una sinusoide completa sarebbero infatti necessarie 360 tacche sull'asse delle ascisse.

La funzione seno non è nè iniettiva nè surittiva. Per renderla biettiva e quindi invertibile, sono necessarie delle opportune restrizioni. In particolare per renderla suriettiva si restringe il codominio all'insieme immagine ovvero l'intervallo tra -1 e 1, per renderla iniettiva si restringe il dominio agli angoli compresi tra -π/2 e π/2. La funzione seno con le dette restrizioni f:[-π/2,π/2]→[-1,1] risulta essere invertibile. Lo si nota, dal punto di vista grafico, poichè su ogni orizzontale, condotta all'interno del rettangolo ottenuto tramite le dette restrizioni, c'è un unico punto di intersezione con la funzione seno. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione seno "ristretta", intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. In figura è riportato il rettangolo, ottenuto con le restrizioni previste, in cui la funzione seno è in blu. La funzione inversa, in rosso, ottenuta dalla detta rotazione della funzione seno, è la funzione arcoseno.

La funzione seno con le dette restrizioni: f: [-π/2,π/2] → [-1,1] è biettiva e quindi invertibile. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione seno ristretta intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. La funzione inversa è la funzione arcoseno.
E' importante notare che la funzione arcoseno ha per insieme immagine l'insieme [-π/2,π/2] per cui quando si la si usa per la risoluzione dei triangoli bisogna tener presente che non apprezza angoli ottusangoli. Oltre ad un eventuale angolo α, ottenuto tramite la funzione bisogna tener conto di un eventuale ulteriore angolo π-α, in quanto sen(α)=sen(π-α).

In figura il grafico della funzione cosx l'unità di misura degli angoli è il radiante. L'insieme immagine della funzione coseno è l'intervallo compreso tra -1 e 1. E' una funzione periodica di periodo 2π. Si può dimostrare che il grafico della funzione coseno ha delle specifiche caratteristiche sempre nel caso in cui l'unità di misura sia il radiante e la scala 1:1. In particolare la tangente in π/2 alla funzione corrisponde alla retta y=-x. Per questo motivo nella rappresentazione della funzione si usa tale unità di misura. Se usassimo il grado il grafico della funzione coseno sarebbe sempre una sinusoide ma molto più "allungata" per eseguire una sinusoide completa sarebbero infatti necessarie 360 tacche sull'asse delle ascisse.

La funzione coseno non è nè iniettiva nè surittiva. Per renderla invertibile, quindi, sono necessarie delle opportune restrizioni. In particolare per renderla suriettiva si restringe il codominio all'insieme immagine ovvero l'intervallo tra -1 e 1, per renderla iniettiva si restringe il dominio agli angoli compresi tra 0 e π.
La funzione coseno con le dette restrizioni f:[0,π]→[-1,1] è biettiva e quindi invertibile. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione coseno ristretta intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. La funzione inversa è la funzione arcocoseno.

La funzione coseno con le dette restrizioni f:[0;,π]→[-1,1] è biettiva e quindi invertibile. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione coseno "ristretta" intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. La funzione inversa è la funzione arcocoseno.

In figura il grafico della funzione tanx l'unità di misura degli angoli è il radiante. L'insieme immagine della funzione tangente è R. E' una funzione periodica di periodo π.

La funzione tangente è suriettiva ma non iniettiva. Per renderla invertibile, quindi, sono necessarie delle opportune restrizioni. Per renderla anche iniettiva si restringe il dominio agli angoli compresi tra -π/2 e π/2
La funzione tangente con la detta restrizione f:[-π/2,π/2]→R è biettiva e quindi invertibile. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione tangente "ristretta" intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. La funzione inversa, in rosso, è la funzione arcotangente.

La funzione tangente con le dette restrizioni f:[-π/2,π/2]→R è biettiva e quindi invertibile. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione tangente "ristretta" intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. La funzione inversa è la funzione arcotangente.

In figura il grafico della funzione tanx l'unità di misura degli angoli è il radiante. L'insieme immagine della funzione tangente è R. E' una funzione periodica di periodo π.

La funzione cotangente è suriettiva ma non iniettiva. Per renderla invertibile, quindi, sono necessarie delle opportune restrizioni. Per renderla anche iniettiva si restringe il dominio agli angoli compresi tra 0 e π
La funzione cotangente con la detta restrizione f:[0,π]→R è biettiva e quindi invertibile. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione cotangente "ristretta" intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. La funzione inversa, in rosso, è la funzione arcocotangente.

La funzione cotangente con le dette restrizioni f:[0,π]→R è biettiva e quindi invertibile. Per disegnare il grafico della funzione inversa è necessario ruotare la funzione cotangente "ristretta" intorno alla bisettrice del primo e terzo quadrante in modo da scambiare l'asse delle ascisse con quello delle ordinare. La funzione inversa è la funzione arcocotangente.