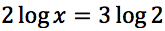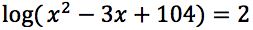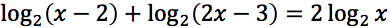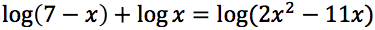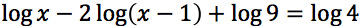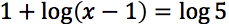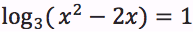Determinare il campo di esistenza delle seguenti funzioni:
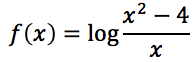
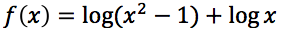
Esercizi guida
Date le funzioni f(x)=3x e g(x)= 2x+3, determinare fog, gof.
Calcolare.
Date le funzioni f(x)=x2 e g(x)= 2x-1, determinare fog, gof.
Date le funzioni f(x)=x2+2x e g(x)= x+2, determinare fog, gof.
Esercizi guida
Data la funzione y= f(x)=3x+2 f(x): R→R determinare le opportune restrizioni per renderla biettiva quindi determinare l'espressione analitica della funzione inversa e il relativo diagramma cartesiano.
La funzione è una retta obliqua quindi è una funzione biettiva. Non è necessaria quindi, alcuna restrizione. Per determinare la funzione inversa va esplicitata la variabile x: -3x=-y+2 da cui x=f-1(y)=(y-2)/3. Si noti che espressa a parole la f si può enunciare in questo modo: "moltiplica per 3 ed aggiungi due". La f-1 a parole si enuncia: "togli due e dividi per tre". A parole l'inversa si ottiene leggendo da destra verso sinistra la f eseguendo le operazioni inverse. A questo punto si rinominano le variabili per cui y=f-1(x)= x/3-2/3. La funzione f-1 dal punto di vista grafico è ottenuta attraverso una simmetria assiale o anche attraverso una rotazione della f rispetto alla bisettrice del primo e terzo quadrante.
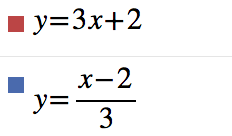
Data la funzione f(x)=x2-1 f(x): [-2,2]→[-2,3] determinare le opportune restrizioni per renderla biettiva quindi determinare l'espressione analitica della funzione inversa e il relativo diagramma cartesiano.
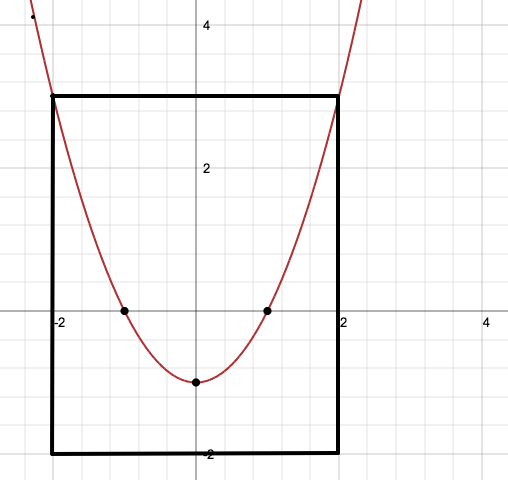
La base e l'altezza del rettangolo, costituiscono rispettivamente il dominio ed il codominio della funzione presa in esame che dal punto di vista grafico è un ramo di parabola.
Si può notare che esistono orizzontali, esattamente quelle del tipo y=k, -1<k≤3 condotte sempre all'interno del rettangolo, che intersecano la funzione in due punti. La funzione non è quindi iniettiva in quanto un elemento dell'insieme immagine è il corrispondente di due elementi del dominio. Si può notare anche che esistono orizzontali, esattamente quelle del tipo y=k, -2≤k<-1 condotte sempre all'interno del rettangolo non intersecano la funzione. Per questo motivo la funzione non è neppure suriettiva poichè ci sono elementi del codominio esattamente i valori compresi tra -2 e -1 che non sono i corrispondenti di alcun elemento del dominio.
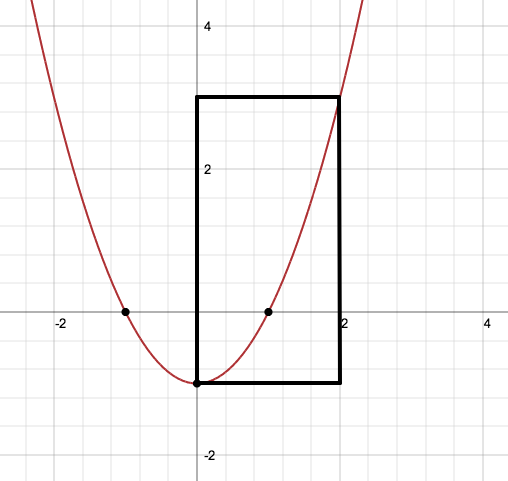
Per rendere la funzione iniettiva bisogna quindi restringere il dominio all'intervallo [0,2] e per renderla suriettiva il codomonio va ristretto all'insieme immagine cioè all'intervallo [-1,3]. f-1 In tal modo restringiamo la funzione a f(x): [0,2]→[-1,3] e nel rettangolo che ha per base il dominio e per altezza il codominio succede che su ogni orizzontale c'è un unico punto della funzione.
In altre parole la funzione con queste restrizioni diventa biettiva e quindi invertibile.
.
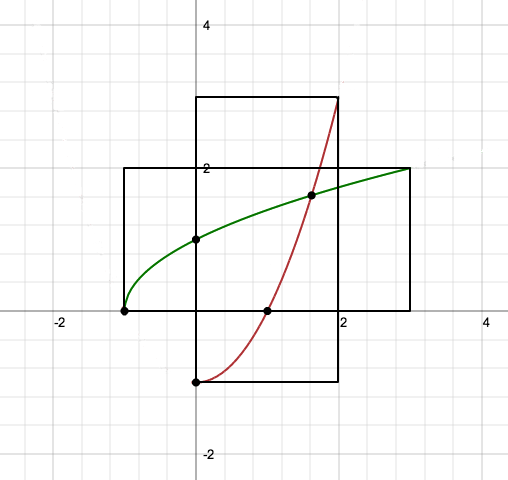
Per individuare l'espressione analitica della funzione inversa va esplicitata la variabile "x" ovvero partendo da: y=f(x)=x2-1 otteniamo x2=y+1 ed infine x=f-1(y)=√y-1.
Per avere sullo stesso sistema di riferimento sia la f(x) che la relativa inversa si rinominano le variabili ottenendo: y=f-1(x)=√x-1. Dal punto di vista grafico la f-1 è quindi ottenuta con una rotazione della f attorno alla bisettrice del primo e terzo quadrante. La rotazione è sinonimo di simmetria assiale si può anche dire che la f-1 è quindi ottenuta con una simmetria della f avente per asse la retta y=x.
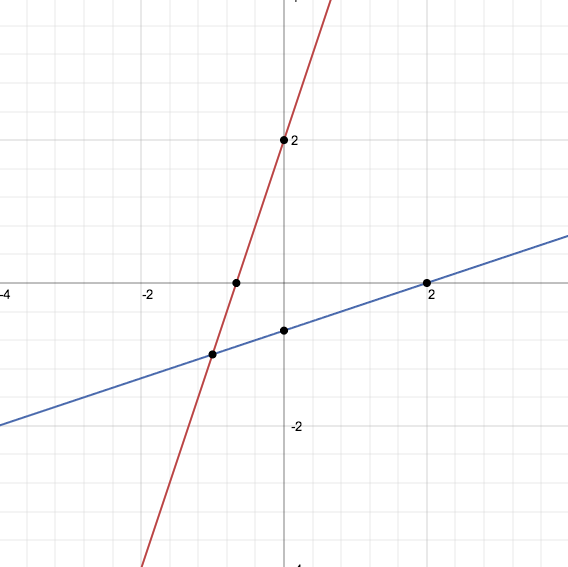
Nella figura si nota la simmetria tra i due rami di parabola che rappresentano rispettivamente la f e la f-1. Si nota che sono stati ruotati pure i rettangoli contenenti le due funzioni.
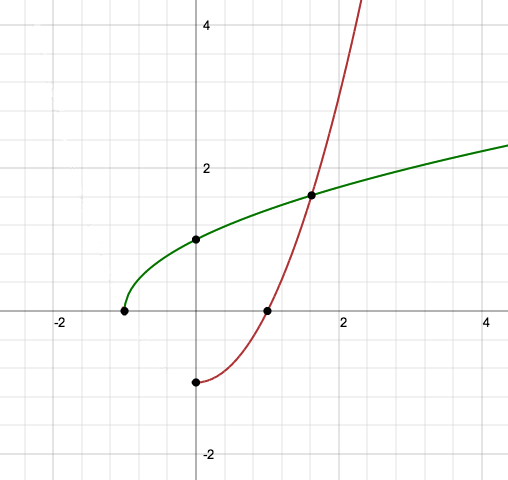
In figura sono riportati i due rami di parabola che rappresentano le due funzioni
legendaData la funzione f(x)=x2-1 f(x): [-1,2]→[-2,5] determinare le opportune restrizioni per renderla biettiva quindi determinare l'espressione analitica della funzione inversa e il relativo diagramma cartesiano.
Tracciare il grafico delle seguenti funzioni:
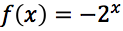
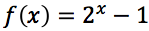
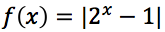
Esercizi guida
Risolvere la seguente equazione:
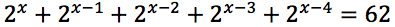
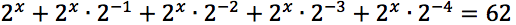
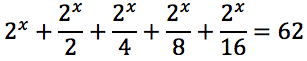
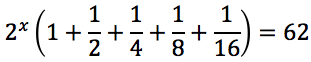
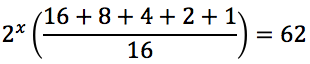
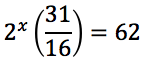
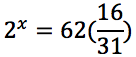
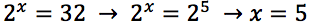
Risolvere la seguente equazione esponenziale.
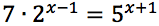
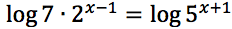
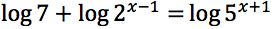
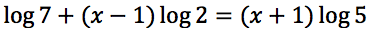
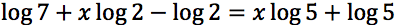
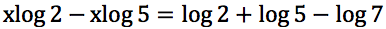
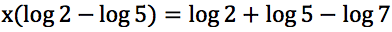
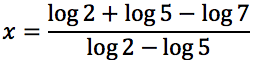
Risolvere le seguenti equazioni:
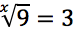
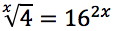
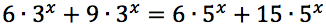
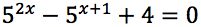
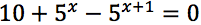
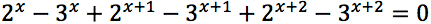
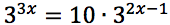

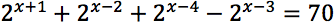
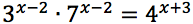
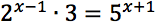
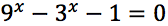
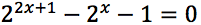
Esercizi guida
Risolvere la seguente equazione applicando la definizione:
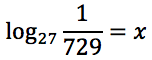
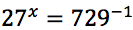
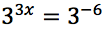
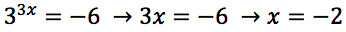
Sviluppare la seguente espressione applicando le proprietà del logaritmo nell'ipotesi che tutti gli argomenti siano positivi.
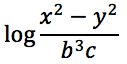
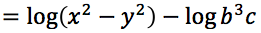
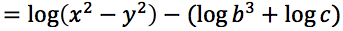
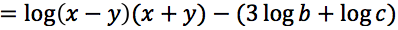
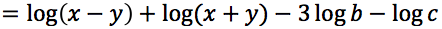
Risolvere le seguenti equazioni applicando la definizione:
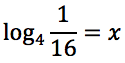
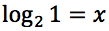
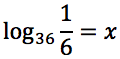
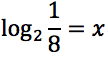
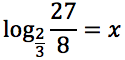
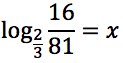
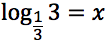
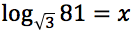
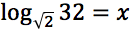
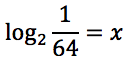
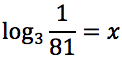
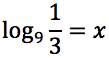
Tracciare il grafico delle seguenti funzioni:
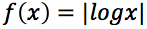
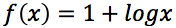
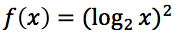
Esercizi guida
Risolvere la seguente equazione
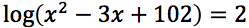
Si noti che l'argomento del logaritmo ha il discriminante minore di zero quindi l'argomento stesso risulta essere sempre maggiore di zero, quindi il campo di esistenza delle soluzioni è tutto l'insieme dei numeri reali.
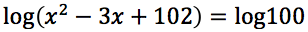
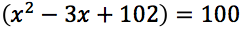
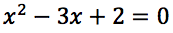
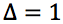
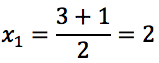
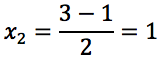
Sia x1 che x2 sono soluzioni accettabili.
Risolvere la seguente equazione
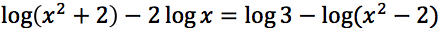
E' necessario che ognuno degli argomenti del logaritmo presenti siano contemporaneamente positivi a tale scopo impostiamo e risolviamo il seguente sistema:
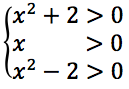
La prima disequazione è verificata per ogni valore reale, la terza per valori reali maggiori di √2 oppure per valori reali minori di -√2, per cui, intersecando le tre soluzioni otteniamo la soluzione del sistema che sono i valori reali maggiori di √2.
Applichiamo ora la quarta proprietà del logaritmo:
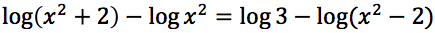
Applichiamo la terza proprietà del logaritmo:
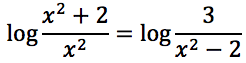
Uguagliamo gli argomenti e otteniamo l'equazione fratta:
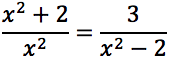
Risolvendo il sistema di sopra è stato già individuato l'insieme in cui i denominatori dell'equazione sono diversi da zero, per cui moltiplicando per il m.c.m. si ottiene:
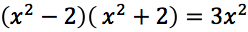
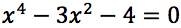
Si tratta di una biquadratica che è riconducibile ad un'equazione di secondo grado con la seguente sostituzione:
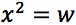
Si ottiene così l'equazione:
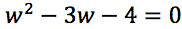
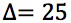

La soluzione w2, essendo negativa, non dà alcuna soluzione, infatti per determinare il relativo valore per l'incognita "x" dovremo eseguire la radice di -1. Le uniche soluzioni dell'equazione biquadratica sono quindi:
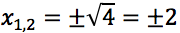
Affinchè una soluzione sia accettabile è necessario che soddisfi alle condizioni trovate risolvendo il sistema per cui l'unica soluzione accettabile per l'equazione logaritmica è x=2
Risolvere le seguenti equazioni: