Blaise Pascal, scienziato e filosofo, (Clermont 1623-Parigi 1662), personaggio eclettico, fondamentale nella sistematizzazione del calcolo combinatorio e nell'introduzione del concetto di probabilità.
Giovanissimo, si dedicò a studi matematici e fisici, elaborando, tra l’altro, una macchina calcolatrice detta pascaline.
Studiò all'università della Sorbona a Parigi, fece ricerche sul vuoto, sulla pressione atmosferica, sull'equilibrio dei liquidi.
Oltre alle importanti intuizioni sul calcolo delle probabilità, condusse studi di geometria, che lo portarono all'enunciazione del teorema che ha il suo nome: le tre coppie di lati opposti di un esagono inscritto in una conica si incontrano in tre punti allineati lungo una retta, detta retta di Pascal.

Ci proponiamo di calcolare il numero delle applicazioni che si possono creare fra due insiemi finiti. Per fare un esempio concreto supponiamo che A sia un insieme di tre oggetti: a, b, c. Ci domandiamo in quanti modi diversi essi possano essere posti in cinque cassetti tenendo presente che possono anche essere contenuti tutti in un unico cassetto. Indichiamo con B = {1,2,3,4,5} l'insieme dei cassetti. Consideriamo l'oggetto a; esso può essere mandato in uno dei cinque cassetti, dunque per quello che riguarda a, ci sono cinque possibilità diverse. Consideriamo ora l'oggetto b: esso può essere mandato in uno qualsiasi dei cinque cassetti, indipendentemente dal modo con cui è stato collocato a. Analogamente si procede per c. Dunque ci sono in tutto 5*5*5 = 125 distinte applicazioni dell'insieme A nell'insieme B.
Possiamo facilmente passare a considerare una situazione generale: A sia un insieme di k oggetti, e B un insieme di n oggetti. Il numero di tutte le applicazioni di A in B è dato da: n*n*n*...*n = n k
Un problema interessante è quello di contare le applicazioni iniettive di A in B. Prendendo un esempio concreto, si tratta di riporre tre oggetti in cinque cassetti, in modo che non ne vada più di uno in ciascun cassetto. Cominciamo con l'oggetto a: esso può essere collocato in uno dei cinque cassetti; quindi ci sono cinque possibilità. L'oggetto b può essere collocato solo in uno dei quattro cassetti rimasti liberi. Quando si tratta di collocare l'oggetto c, sono già stati impegnati due cassetti, quindi ci sono solo tre possibilità. Dunque, il numero delle applicazioni iniettive di un insieme di tre elementi in un insieme di cinque elementi è: 5*4*3 = 60 (Naturalmente, il numero è inferiore a quello dell'insieme delle applicazioni arbitrarie). Consideriamo ora il caso generale: A è un insieme di k elementi, B un insieme di n elementi. Se si vuole che siano possibili applicazioni iniettive, deve essere k minore di n, nell'esempio il numero dei cassetti non deve essere inferiore a quello degli oggetti. Possiamo ripetere, in termini generali, il ragionamento fatto: per collocare il primo oggetto di A ci sono n possibilità, per collocare il secondo oggetto di A ci sono n-1 possibilità, per collocare il terzo oggetto di A ci sono n-2 possibilità. Dunque il numero delle applicazioni iniettive, che indicheremo con D(n,k) è dato dalla formula: D(n,k) = n(n-1)(n-2)...(n-k+1).
Supponiamo di dover disporre n studenti in n banchi mettendo in ogni banco un unico studente,
si tratta di disposizioni semplici in cui è n=k.
In questo caso, il numero di elementi di A è uguale al numero degli elementi di B e il numero cercato
corrisponde a quello delle applicazioni biiettive che si possono costruire quando il dominio è A ed
il codominio B.
Le applicazioni di questo tipo vengono dette permutazioni. Sempre in questo caso si può pensare
che l'insieme A corrisponda all'insieme B per cui le permutazioni vengono anche dette
sostituzioni nell'insieme A in sè.
Tornando all'esempio iniziale, il primo studente potrà scegliere n banchi,
il secondo trovando già occupato un banco ne potrà scegliere n-1 e così via fino all'ultimo studente che
dovrà disporsi nell'ultimo posto rimasto libero.
Il numero delle permutazioni è quindi dato da: n(n-1)(n-2)...3*2*1 cioè dal prodotto dei primi n interi, a partire da 1.
Questo prodotto si chiama fattoriale di n e si scrive n!
In opere cinesi del 1100 circa si fa riferimento a sistemi di tabulazione per coefficienti dello sviluppo della potenza di un binomio: è verosimile che quella tabella di numeri, nota in occidente con il nome di "triangolo di Pascal" o "triangolo di Tartaglia" abbia avuto origini in Cina intorno a tale data.
Niccolò Tartaglia, matematico (Brescia ca. 1499-Venezia 1557). Legò il suo nome alla scoperta della formula risolutiva dell'equazione di 3° grado ad un'incognita.
Da fanciullo era stato ferito alla bocca da una sciabolata di un soldato francese, durante la battaglia che nel 1512 portò Brescia, che era sotto il dominio di Venezia, nelle mani dei francesi. Questa ferita danneggiò le sue capacità di parlare e per questo venne soprannominato Tartaglia, nome che in seguito egli usò invece di quello di Nicolò Fontana che gli era stato dato dalla nascita.
La cosa interessante è che il famoso triangolo servì a Tartaglia, per calcolare i coefficienti dello sviluppo del binomio elevato alla n-esima potenza.

| 1 | ||||||||||||||||||
| 1 | 1 | |||||||||||||||||
| 1 | 2 | 1 | ||||||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||||||||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
C(n,k)=C(n,n-k)
La seconda proprietà è che, ogni numero di una certa riga è dato dalla somma dei due numeri che si trovano nella precedente riga, il primo nella stessa diagonale, il secondo nella diagonale sucessiva. Questa caratteristica si riassume nella seguente formula:
C(n,k)=C(n-1,k)+C(n-1,k-1)
I numeri del triangolo rappresentano le "combinazioni" ovvero il numero di sottoinsiemi di k elementi in un insieme di n elementi.
Con la tabella possiamo, dato un insieme di cinque elementi, determinare quanti sono i suoi sottoinsiemi di due elementi. Per esempio se numeriamo questi oggetti dal numero uno al cinque ogni riga della tabella rappresenta un diverso sottoinsieme. Possiamo concludere che 10 esprime il numero dei sottoinsiemi di 2 elementi che si possono prendere in un insieme di 5 elementi.
Sarebbe lo stesso prendere i sottoinsiemi di tre elementi: infatti, basta cancellare gli "X" e mettere le "X" nelle caselle vuote che si trova la tabella con i sottoinsiemi complementari dei precedenti. C(n,k) viene detto anche numero delle combinazioni di n elementi di classe k ed è il numero del triangolo che si trova all'incrocio della n-esima riga con la k-esima diagonale.
Il ragionamento fatto ci ha anche mostrato chiaramente che è:
(5,3) = (5,2)
questo perche in un insieme di 5 elementi sceglierne 2, equivale a scartarne 3, inoltre tutto ciò viene confermato anche dalla simmetria del triangolo di Tartaglia-Pascal.
| 1 | 2 | 3 | 4 | 5 |
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X | |||
| X | X |
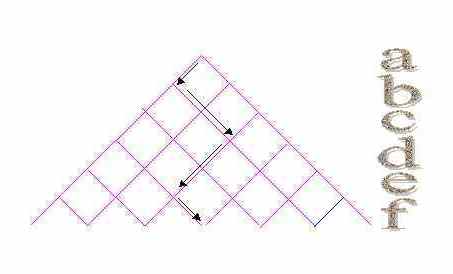
Si può anche pensare di associare ad un determinato percorso un sottoinsieme, "vai a destra" potrebbe voler dire che l'elemento di quel livello appartiene al sottoinsieme, "vai a sinistra" invece, che non appartiene al sottoinsieme.
Per esempio consideriamo come insieme universo, {a, b, c, d, e, f} il percorso della figura di destra corrisponde al sottoinsieme {b, c, f}.
Il numero C(n,k) che è il numero che si trova all'incrocio della n-esima riga e k-esima diagonale del triangolo di Tartaglia-Pascal è detto numero delle combinazioni di n elementi di classe k.
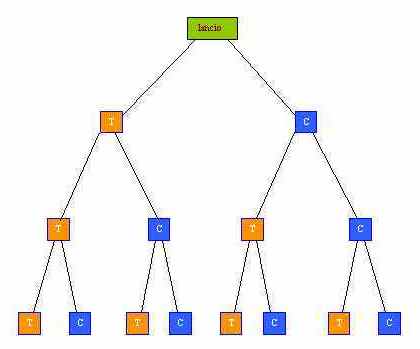
Lancio della moneta
Lanciamo una, due, tre volte una moneta. Gli eventi possibili sono rappresentati dalla tabella o dai vari cammini di un grafo ad albero come in figura. Essi possono essere elencati così, indicando con T "testa" e con C "croce": In tutto sono 8. Gli eventi che si possono verificare nel lancio di una moneta n volte sono 2n: infatti, per n = 1 sono 2: T, C, e ad ogni lancio il numero degli eventi precedentemente elencati è raddoppiato. Per esempio se lanciamo otto volte una moneta ci saranno 256 casi possibili, se poi ci chiediamo quante volte può verificarsi l'evento: 2 teste, 6 croci, dovremo ricercare il secondo elemento, contando a partire dallo zero, della ottava riga del triangolo che è 28, oppure il sesto elemento della stessa riga, che è comunque sempre 28. In generale, consideriamo ora il caso di n lanci: ci chiediamo in quanti casi T si presenta k volte (essendo, naturalmente, 0≤k≤n) e, ovviamente, C si presenta n-k volte. A questo scopo, conviene fare ricorso ad un tipo di grafo, più espressivo, che non è più "ad albero". In questo grafo, i cammini diversi che arrivano ad uno stesso vertice contengono uno stesso numero di T e di C, in ordine diverso. Ad esempio per n=3, il vertice che corrisponde a "2 volte T ed una volta C", viene raggiunto attraverso 3 cammini.
| T | T | T |
| T | T | C |
| T | C | T |
| C | T | T |
| C | C | T |
| C | T | C |
| T | C | C |
| C | C | C |
Il numero dei percorsi in una città a pianta romana ... per la via più breve
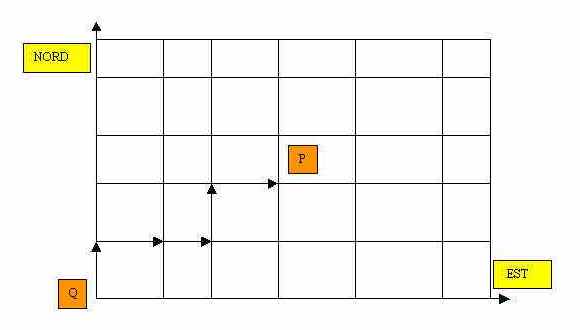
Risolviamo un piccolo problema: la pianta di una città sia come nella figura; le linee orizzontali e verticali rappresentano le vie. Un turista parte dal punto Q; ad ogni incrocio egli va, a caso, verso est oppure verso nord (lanciando una moneta). La situazione è solo in apparenza diversa da quella considerata nel lancio di una moneta; in realtà, basta intendere che T significhi tratto verso e C tratto verso nord. I numeri di Pascal ci dicono in questo caso in quanti modi diversi, per la strada più breve, posso giungere per esempio all'incrocio P.
Possiamo osservare, in linea generale, che uno dei vantaggi più forti che ci dà una formazione matematica, è quello di riconoscere che, in molti casi, situazioni all'apparenza diverse hanno una stessa struttura astratta e possono essere chiarite con lo stesso ragionamento. Nel nostro caso, dunque, il numero delle strade che arrivano a P è dato da:(5,3)=(5,2)=10
Una pallina che scende in una serie di canaletti
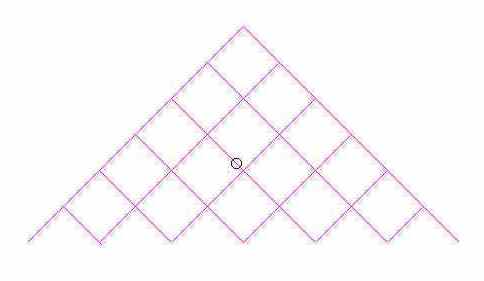
Si pensi che le linee in figura siano canalini nei quali possa correre una pallina la quale, situata inizialmente in cima, cada. Si supponga che, ad ogni bivio non vi siano ragioni per ritenere che la pallina proceda verso destra, piuttosto che verso sinistra.
Si vuole determinare la probabilità che, ad un certo livello, la pallina venga a trovarsi in un certo vertice A(k). Ragionando come nella determinazione del numero di strade che portano ad un certo incrocio, possiamo contare il numero dei casi favorevoli, quindi C(n,k), mentre i casi possibili si otterranno dalla somma di tutti i numeri del livello n-imo in altre parole 2n.
Anagrammi di parole che contengono solo due lettere
| A | A | M | M | M |
| A | M | A | M | M |
| A | M | M | A | M |
| A | M | M | M | A |
| M | A | A | M | M |
| M | A | M | A | M |
| M | A | M | M | A |
| M | M | A | A | M |
| M | M | A | M | A |
| M | M | M | A | A |
Volendo fare gli anagrammi, anche privi di significato, della parola mamma compiliamo una tabella come quella in figura.
La somiglianza con una tabella come quella che individua i sottoinsiemi di due elementi in un insieme di cinque elementi è notevole: basta sostituire alle “A” le “X” e non mettere niente al posto della “M” che le tabelle sono uguali.
In altre parole in un insieme di cinque caselle, bisogna scegliere i sottoinsiemi di due caselle nei quali inserire la lettera A, nelle altre caselle poi, inseriremmo la lettera M.
Quindi il numero di anagrammi della parola mamma sarà uguale al numero di Pascal che si trova nella quinta riga e seconda diagonale del triangolo ovvero corrisponde al numero di colonne della tabella in figura cioè 10.
Il ragionamento ci permette quindi, di determinare quanti sono gli anagrammi di quelle parole come nonno, Anna, non, papà, composte da due sole lettere.
Cerchiamo di determinare C(n,k), ovvero un numero del triangolo di Tartaglia Pascal attraverso una formula,
senza dover compilare tutte le righe precedenti alla n-esima. Ci aiutiamo risolvendo un semplice problema.
Il problema è il seguente: in quanti modi possiamo disporre k studenti in n banchi, pensando che ogni
studente può occupare un unico banco e che il numero degli studenti sia minore al numero dei banchi.
Risolviamo il problema in due modi diversi.
primo ragionamento: possiamo pensare che il primo studente, che sceglie il banco, può farlo in
n modi, il secondo trovando un banco già occupato può farlo in n-1 modi,
il terzo trovando due banchi già occupati può farlo in n-2 modi e così via, fino a che, l'ultimo,
cioè il k-eimo studente, trovando n-(k-1) banchi già occupati, può
scegliere tra gli n-k+1 banchi rimasti. In definitiva si tratta di disposizioni semplici ed il numero
che si ottiene è: n(n-1)(n-2) ... (n-k+1)
secondo ragionamento: si può anche partire pensando a come sarà la disposizione finale degli
studenti.
Quando tutti avranno scelto il banco, ci saranno k banchi occupati da k studenti, quindi innanzitutto,
bisogna conteggiare in quanti modi diversi si possono scegliere i k banchi che saranno occupati dai k
studenti. In altre parole bisogna conteggiare quanti sono i sottoinsiemi di k banchi in un insieme di
n banchi. Ovviamente il numero è quello che si trova all'incrocio della n-esima riga con la k-esima
diagonale del triangolo di Tartaglia Pascal cioè le combinazioni C(n,k). Una volta scelti i k banchi
che saranno occupati, bisogna pensare in quanti modi diversi i k studenti possono disporsi nei k banchi.
Si tratta di permutazioni per cui il numero è: k!, quindi con questo ragionamento otteniamo: C(n,k)k!
Anche se il secondo ragionamento è un pò più complicato del primo, risulta comunque valido, e deve
produrre lo stesso risultato, per cui si
potrà scrivere: C(n,k)k!=n(n-1)(n-2) ... (n-k+1).
A questo punto ci si comporta come se quella
scritta fosse un'equazione di primo grado avente per incognita C(n,k). Risolta l'equazione si trova che:
C(n,k) = n(n-1)(n-2) ... (n-k+1)/k!
Il triangolo di Tartaglia consente di individuare i coefficienti dello sviluppo di un binomio (a+b) elevato alla n-esima potenza. I coefficienti dei singoli termini sono dati dai numeri della (n+1)-esima riga del triangolo. Proponiamoci di sviluppare l'espressione (x+y)2, dove n è un intero positivo (potenza n-sima del binomio). Sappiamo che si ha (x+y)2 =x2 + 2xy + y2 e con un semplice calcolo si trova: (x+y)3 =x3+3x2y+3xy2+ y3
I monomi che si ottengono dallo sviluppo di (x+y)2 e di (x+y)3 li possiamo rappresentare mediante un grafo simile a quello della figura
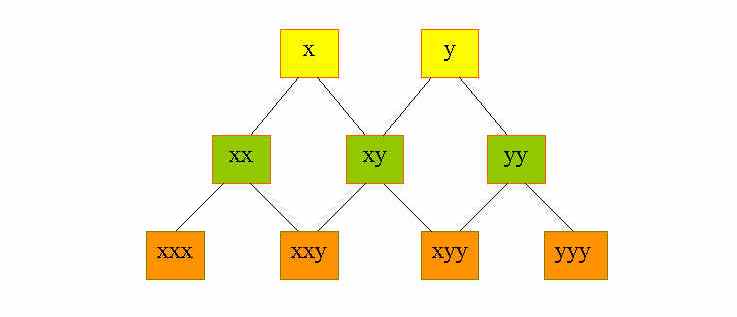
ad ogni cammino sul grafo corrisponde un monomio, per esempio il percorso sinistra sinistra destra partendo da sopra corrisponde al monomio xxy. Il grafo sembra analogo a quello che rappresenta il lancio della moneta. Per la proprietà commutativa della moltiplicazione, due monomi contenenti lo stesso numero di volte le x, e le y, diventano simili. Ad esempio, i due monomi xyx e xxy sono simili. Il problema è allora quello di contare i monomi che diventano simili traloro. Conviene quindi modificare il grafo facendo confluire in uno stesso vertice i cammini che corrispondono a monomi simili. Il nostro problema si riduce a quello di contare il numero dei cammini che arrivano ad un dato vertice in un grafo come quello della figura. Detto questo, il nostro problema risulta perfettamente analogo a quello di contare i percorsi della pallina che scende nei canaletti. Notiamo quindi le analogie tra eventi, anche molto diversi tra loro come lancio monete, conteggio percorsi in una città a pianta romana, conteggio percorsi della pallina che scende nei canaletti, anagrammi di parole formate da due lettere, sviluppo del binomio. Teniamo presente che, quando conteggiamo dei percorsi, intendiamo sempre che si parte da sopra e si percorre la via più breve per arrivare ad un certo incrocio.
Possiamo concludere così: lo sviluppo di (x+y)n è costituito dalla somma di tutti i monomi del tipo xn-k yk moltiplicati per i coefficienti (n,k) che sono i numeri del triangolo di Tartaglia-Pascal.
Ricordiamo che è: (n,n) = (n,0) = 1 (n,1) = (n,n-1) = n
Indichiamo con n il numero delle righe,
tenendo presente che la prima riga, quella con il solo numero 1 è la riga zero. Indichiamo con k il numero delle diagonali,
tenendo presente che la prima diagonale, quella formata da tutti numeri 1, è la diagonale zero.
Sviluppando (x+y)5 otteniamo x5+5x4y+10x3y2+10x2y3+5xy4+y5.
Prova è l'esecuzione di un esperimento.
U, insieme universo delle probabilità, associato ad un dato esperimento, è l'insieme dei risultati possibili.
Evento è un insieme di risultati possibili, ovvero un sottoinsieme di U.
Evento elementare è sottoinsieme di U con un solo elemento.
Evento certo, è quello che si realizza sempre.
Evento impossibile, è quello che non si realizza mai.
lancio di 8 monete
(9 risultati possibili): 8 teste; 7 teste 1 croce; 6 teste 2 croci; 5 teste 3 croci; 4 teste 4 croci; 3 teste 5 croci; 2 teste 6 croci; 1 testa 7 croci; 8 croci.
escono almeno 2 teste.
escono 2 teste e 6 croci.
escono al massimo 8 teste.
escono almeno 9 teste.
Si esegue un grande numero di prove. Per esempio si fanno 10000 lanci con 8 monete e si conta la frequenza assoluta, ovvero gli "n" casi in cui sono uscite 2 teste e 6 croci, quindi si calcola la probabilità attraverso il rapporto n/10000. In questo modo la probabilità assume l'aspetto di frequenza relativa.
La probabilità è uguale al rapporto tra i casi favorevoli ad un certo evento E ed i casi possibili pensati come egualmente probabili. Per esempio se l'esperimento è il lancio di 8 monete, il numero dei casi possibili è 28=256. Se l'evento è: uscita di 2 teste e 6 croci, il numero dei casi favorevoli è 28, ossia il numero che si trova nel ottava riga, seconda diagonale del triangolo di Tartaglia Pascal. La probabilità quindi che lanciando 8 monete, escano 2 teste e 6 croci è: P(E)=28/256. Si tenga presente che la probabilità è un numero razionale compreso tra 0 e 1 ovvero 0≤P(E)≤1.
Nella tabella sono riportati i grafici della frequenza relativa e della probabilità dell'esperimento: lancio di otto monete.
Tramite il foglio elettronico (con la variabile "casuale") si sono simulati 500 lanci di otto monete e si è conteggiato (con la funzione "conta.se") il numero di volte che si è verificato l'evento: 0 teste 8 croci, 1 testa 7 croci, 2 teste 6 croci, 3 teste 5 croci, 4 teste 4 croci, 5 teste 3 croci, 6 teste 2 croci, 7 teste 1 croce, 8 teste 0 croci. La frequenza relativa si è calcolata dividendo la frequenza assoluta per 500. Per il calcolo della probabilità invece i casi possibili sono i numeri della ottava riga del triangolo: 1, 8, 28, 56, 70, 56, 28, 8, 1, i casi possibili sono 28=256.
La probabilità è stata calcolata quindi: P(E)=casi possibili/casi favorevoli.
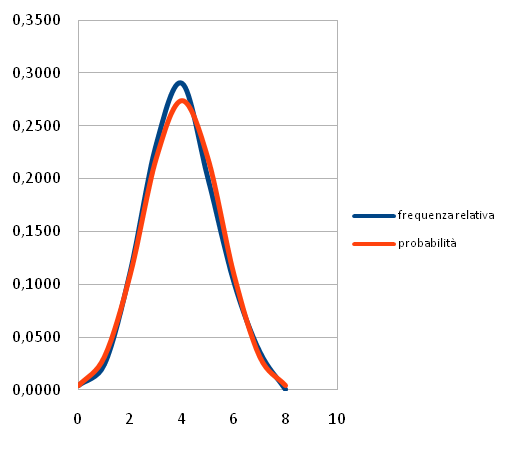
Se avessimo fatto la simulazione di 10000 lanci i due grafici sarebbero risultati praticamente sovrapposti. Si noti ancora che si tratta di grafici a "campana" con picco sull'evento 4 teste e 4 croci che ovviamente è il più probabile.
Però c'è da sottolineare che non tutti gli eventi sono ripetibili; ad esempio, una partita di pallacanestro di cui vogliamo calcolare la probabilità della vittoria della squadra X contro la squadra Y.
La definizione di probabilità applicabile ad esperimenti casuali i
cui eventi elementari non siano ritenuti ugualmente possibili e che non siano necessariamente ripetibili più
volte sotto le stesse condizioni è dovuta ad Bruno de Finetti.
Bruno De Finetti, che ha insegnato matematica anche all'università degli studi di Trieste,
dove c'è un'aula a lui dedicata, ha proposto la concezione soggettiva della probabilità.
La probabilità di un evento è il prezzo che un individuo ritiene equo pagare per ricevere 1 se l'evento si verifica, 0 se l'evento non si verifica.
Esempio: se penso che le probabilita' di vincita in una partita di pallacanestro della squadra X contro la squadra Y siano del 60%, devo essere disposto a puntare 60 euro, sulla sua vincita, per riceverne 100 in caso di vittoria e perdendo tutto in caso di sconfitta. E' fondamentale, che devo avere il maggior numero di informazioni possibili e, tramite esse, devo attribuire determinate probabilita' a determinati eventi. Nel caso specifico devo sapere come sono in classifica, chi gioca in casa, se ci sono giocatori assenti per infortunio, qual'è lo stato di forma delle due squadre ecc.. ecc..
La dedizione ossessiva a slot machine, videopoker e gratta e vinci sottrae agli italiani molte risorse e provoca una serie di gravi problemi. Lo Stato, che comunque incassa le tasse, si ritrova a pagare elevati costi socio-sanitari per la cura dei ludopatici. L'indebitamento dei giocatori patologici favorisce inoltre, l'usura e l'adescamento da parte della criminalità di giocatori malati.
Senza dimenticare questo, nelle prossime righe ci occuperemo, solo ed esclusivamente, del calcolo delle probabilità legato a due giochi quali il poker e i dadi.
Il poker classico si pratica in 4 giocatori con 32 carte cioè 7, 8, 9, 10, J, Q, K, A. Se il numero di giocatori non è 4, ma 3 o 5 allora la carta più bassa è quella risultante dalla differenza fra 11 e il numero dei giocatori. Nel poker all'americana, invece si usano tutte le 52 carte. Si può notare quindi, analizzando i calcoli fatti sotto, quella che può sembrare una contraddizione, ovvero che, nel gioco classico, il poker è più probabile del colore. Il motivo per cui il colore vale meno del poker è dovuto al fatto che la scala di valori viene costruita in base alla probabilità del gioco all'americana dove, giocando con 52 carte le probabilità sono diverse.
Calcoliamo tutte le probabilità pensando di avere in mano cinque carte scelte a caso dal mazzo.
Applichiamo ovviamente la formula: P(E) = casi favorevoli/casi possibili.
Il numero di casi possibili é: C(52,5) = 2.598.960
infatti bisogna determinare il nimero di sottoinsiemi di 5 elementi in un insieme di 52.
Partiamo dagli eventi meno probabili:
I casi favorevoli per "fare" scala reale sono: A 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 5 6 7 8 9 6 7 8 9 10 7 8 9 10 J 8 9 10 J Q 9 10 J Q K 10 J Q K A. Sono dunque 10 le possibili scale che vanno moltiplicate per il numero dei semi per ottenere i casi favorevoli ovvero 40. La probabilità è quindi:
p(E) = 40/2.589.960 = 0,000015
Sono 13 i possibili modi di fare poker, questo numero va moltiplicato per il numero che si ottiene sottraendo a 52, che è il numero totale delle carte, le carte usate per il poker. Si moltiplica quindi 13 per 48 che sono i diversi modi di scegliere la quinta carta, la probabilità sarà quindi:
p(E) = 13*48/2.598.960 = 624/2.598.960 = 0,00024
Il tris si può fare in 13 modi diversi moltiplicati per C(4,3), la coppia in 12 moltiplicando per C(4,2) e dividiamo poi per i casi possibili:
p(E) = 13*12*C(4,3)*C(4,2)/2.598.960 = 52*72/2.598.960 = 3.744/2.598.960 = 0.0014
Moltiplicando i modi in cui si possono scegliere 5 carte in un insieme di 13 carte per i 4 semi e sottraendo alla moltiplicazione il numero 40, che rappresenta tutte le possibili scale reali, si ottengono i casi favorevoli:
p(E) =(C(13,5)*4-40)/2.598.960 = 5.108/2.598.960 = 0,0019
Le scale sono 10, ciascuna delle carte della scala può essere scelta in 4 modi e quindi si moltiplica ancore per il numero 4 elevato alla quinta, infine si sottrae il numero di scale reali che sono 40:
p(E) = (10*45-40)/2.598.960 = 10.200/2.598.960 = 0,0039
Il tris può essere scelto in 13 modi diversi, questo numero va moltiplicato per C(4,3) che rappresenta i sottoinsiemi di 3 carte in un insieme di 4 carte poi si moltiplica per i modi in cui si possono scegliere le rimanenti due carte in un insieme di 12 moltiplicando quindi due volte per 4,cioè i modi in cui si possono scegliere quelle 2 carte:
p(E) = (13*C(4,3)*C(12,2)*42)/2.598.960 =(13*4*66*16)/2.598.960 = 54.912/2.598.960 = 0,021
I casi favorevoli della doppia coppia si ottengono moltiplicando il numero di modi in cui si possono scegliere le due carte con cui fare le 2 coppie ovvero 2 carte in un insieme di 13, moltiplicando questo numero per i modi con cui posso scegliere 4 carte in un insieme di 2, per due volte, dato che le coppie sono 2, moltiplicando ancora il tutto per 44, cioè il numero totale delle carte meno le 8 le utilizzate per le due coppie:
p(E)= (C(13,2)*C(4,2)*C(4,2)*44)/2.598.960 = 78*6*6*44/2.598.960 = 123.552/2.598.960 = 0,047
Per calcolarne la probabilità si procede moltiplicando il numero delle carte per seme che sono 13, per i modi con cui si possono scegliere 2 carte in un insieme di 4 e, poi per scegliere le ultime 3 carte facendo in modo che siano diverse tra loro per cui si devono conteggiare i sottoinsiemi di 3 carte in un insieme di 12 ovvero le carte per seme meno quella usata per la coppia, moltiplicando quindi tre volte per 4 poichè ognuna delle restanti tre carte si possono scegliere in 4 modi:
p(E)=13*C(4,2)*C(12,3)*43/2.598.960 = 1.098.240/2.598.960 = 0,422
Il numero di casi possibili é: C(32,5) = 201.376.
Partiamo dagli eventi meno probabili:
Le possibili combinazioni per avere una scala reale sono: A 7 8 9 10 7 8 9 10 J 8 9 10 J Q 9 10 J Q K 10 J Q K A Ovvero le scale sono 5 che moltiplicato per 4, che rappresenta il numero dei semi, dà i casi favorevoli che sono 20, la probabilità di avere una scala reale sono:
20/201.376 = 0,00009 = 0,009%
Le probabilità del colore si ottengono moltiplicando i modi in cui si possono scegliere 5 carte in un insieme di 8 elementi, poi moltiplicando il numero per 4 cioè il numero dei semi e sottraendo al tutto 20, cioè le possibili scale reali:
((C(8,5)*4)-20)/201.376 = (224-20)/201.376 = 204/201.376 = 0,00101
Moltiplico le carte per seme che sono 8, per il numero totale delle carte del mazzo meno le carte usate per il poker che sono 4 e divido tutto per i casi possibili:
8*28/201.376 = 224/201.376 = 0,00111 = 0,11%
Il tris lo posso fare in 8 modi, questo numero va moltiplicato per 7 che sono i modi secondo cui posso fare la coppia, si moltiplica ancora per i modi in cui si possono scegliere 3 carte in un'insieme di quattro, cioè il tris e poi i modi in cui si possono scegliere 2 carte in un'insieme di 4, per la coppia:
(8*7*C(4,3)*C(4,2))/201.376 = 1.344/201.376 = 0,0066
Le scale sono 5, ciascuna delle carte della scala può essere scelta in 4 modi e quindi si moltiplica ancore per il numero 4 elevato alla quinta, infine si sottrae il numero di scale reali che sono 20:
(5*45-20)/201.376 = 5.100/201.376 = 0,025
Basta moltiplicare le carte per seme per i modi in cui si possono scegliere le tre carte del tris in un'insieme di 4 elementi e poi i modi in cui si possono scegliere le ultime due carte nelle carte rimanenti, ovvero 7 e poi moltiplicando ancora per quattro al quadrato, che sono i modi in cui si possono scegliere le 2 carte nei diversi semi:
8*C(4,3)C(7,2)*42/201.376 = 8*4*21*16/201.376 = 10.752/201.376 = 0,053
La probabilità della doppia coppia si ottiene moltiplicando il numero di modi in cui si possono scegliere le due carte con cui fare le 2 coppie ovvero 2 carte in un insieme di 8, moltiplicando questo numero per i modi con cui posso scegliere 4 carte in un insieme di 2, per due volte, dato che le coppie sono 2, moltiplicando ancora il tutto per 24, cioè il numero totale delle carte meno le 8 le utilizzate per le due coppie, dividendo tutto per i casi possibili:
(C(8,2)*C(4,2)*C(4,2)*24)/201.376 = 28x6x6x24/201.376 = 24.192/201.376 = 0,12
Per calcolarne la probabilità si procede moltiplicando il numero delle carte per seme che sono 8, per i modi con cui si possono scegliere 2 carte in un insieme di 4 e, poi per scegliere le ultime 3 carte facendo in modo che siano diverse tra loro per cui si devono conteggiare i sottoinsiemi di 3 carte in un insieme di 7 ovvero le carte per seme meno quella usata per la coppia, moltiplicando quindi tre volte per 4 poichè ognuna delle restanti tre carte si possono scegliere in 4 modi:
8*C(4,2)*(7,3)*43/201.376 = 8*6*35*64/201.376 = 107.520/201.376 = 0,53
Nel 1600 era molto diffuso un gioco d'azzardo con tre dadi e ovviamente si pose il problema di sapere su quale uscita fosse più conveniente scommettere. I giocatori di quell'epoca non sapendo come regolarsi, eseguivano un gran numero di lanci ed in pratica calcolavano la frequenza relativa delle varie uscite. Si noti che lanciando tre dadi le uscite variano da 3 a 18. A volte però i dadi non erano proprio perfetti, o forse i lanci non erano così numerosi da capire come poteva variare la frequenza, al punto che qualcuno pensò che il 9 ed il 10 uscissero con la stessa probabilità. Fu proprio Pascal, al quale si rivolse un amico per chiedere lumi sul problema, a sistematizzare il tutto e, dalla soluzione di questo ed altri problemi, nacque il calcolo delle probabilità.
| uscite | casi favorevoli | probabilità |
| 3 | 1 | 0,00463 |
| 4 | 3 | 0,013889 |
| 5 | 6 | 0,027778 |
| 6 | 10 | 0,046296 |
| 7 | 15 | 0,069444 |
| 8 | 21 | 0,097222 |
| 9 | 25 | 0,115741 |
| 10 | 27 | 0,125 |
| 11 | 27 | 0,125 |
| 12 | 25 | 0,115741 |
| 13 | 21 | 0,097222 |
| 14 | 15 | 0,069444 |
| 15 | 10 | 0,046296 |
| 16 | 6 | 0,027778 |
| 17 | 3 | 0,013889 |
| 18 | 1 | 0,00463 |
| totale | 216 | 1 |
Nella tabella sono riportate, nella prima colonna le uscite che, come già detto, vanno da 3 a 18, nella seconda colonna sono calcolati i casi favorevoli, nella terza la probabilità. Sommando tutti i casi favorevoli otteniamo 216 che sono i casi possibili come si nota nell'ultima riga della tabella.
Calcoliamo i casi possibili. Si tratta di disposizioni con ripetizione, infatti lanciando il primo dado le uscite possibili sono 6, lanciando il secondo 6, lanciando il terzo ancora 6, per un totale di 63=216.
Questo numero è uguale anche al numero di applicazioni che si possono creare nel caso in cui il dominio sia composto da 3 elementi ovvero il numero dei lanci, ed il codominio da 6 elementi, ovvero il numero delle facce del dado.
Vediamo ora come calcolare quanti sono i casi favorevoli all'uscita del 10, lasciando il calcolo di tutti gli altri eventi per esercizio.
Il 10 può realizzarsi con:
541 ... in 6 modi che sono le permutazioni di tre cifre tutte diverse: 541, 514, 415, 451, 145, 154.
532 ... in 6 modi: 532 523, 325, 352, 235, 253.
631 ... in 6 modi: 631, 613, 361, 316, 136, 163.
622 ... in 3 modi: 622, 262, 226.
442 ... in 3 modi: 442, 424, 244.
334 ... in 3 modi: 334, 343, 433.
Per un totale di 27 casi possibili.
Per il calcolo della probabilità bisogna poi dividere 27 per 216 che è il numero dei casi possibili.
Sommando le probabilità di tutti i casi otteniamo 1.
Nella figura sono riportati i grafici della frequenza relativa e della probabilità dell'esperimento: lancio di tre dadi. Tramite il foglio elettronico (con la variabile "casuale") si sono simulati 1000 lanci di tre dadi e si è conteggiato (con la funzione "conta.se") il numero di volte che si è verificato come somma delle tre facce l'evento: 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.
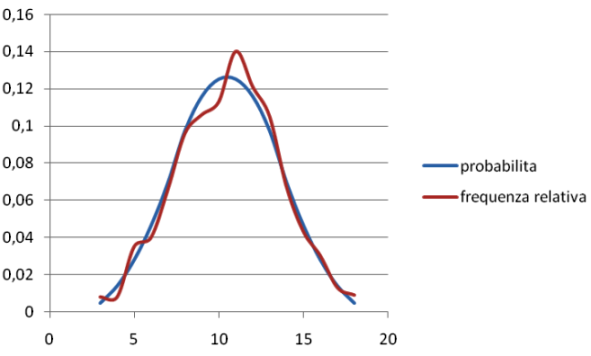
La frequenza relativa si è calcolata dividendo la frequenza assoluta per 1000. La probabilità è stata calcolata quindi con la formula: P(E)=casi possibili/casi favorevoli.
Se avessimo fatto la simulazione di 10000 lanci i due grafici sarebbero risultati praticamente sovrapposti. Si noti ancora che si tratta di grafici a "campana" con picco sull'evento 10 e 11 che sono i più probabili.