La trigonometria, dal greco trìgonon (triangolo) e metròn (misura), è la parte della matematica dedicata allo studio delle relazioni intercorrenti tra gli elementi dei triangoli. Per "elementi" di un triangolo si intendono lati ed angoli. In pratica il problema è quello di calcolare le misure degli elementi di un triangolo avendo come dati iniziali tre misure note, di cui almeno una sia la lunghezza di un lato. Tale problema è indicato come risoluzione del triangolo.
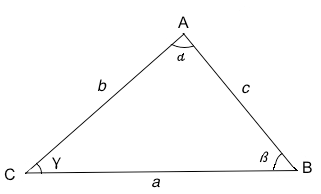
Per risolvere i triangoli ci si serve delle funzioni trigonometriche, con le relative funzioni inverse, a tal proposito si veda grafici delle funzioni goniometriche. Saranno pure indispensabili i teoremi dei seni e del teorema del coseno. Nei problemi che seguono faremo sempre riferimento ad un triangolo come quello di sotto nel quale i vertici vengono indicati con le lettere maiuscole, i lati con le minuscole, gli angoli con le lettere greche. Si noti che il vertice A sta di frote al lato a ed all'angolo α, che il vertice B sta di fronte al lato b ed all'angolo β, e che il vertice C sta di frote al lato c ed all'angolo γ. L'unita' di misura usata nel calcolo degli angoli è il grado a tal proposito si veda unità di misura degli angoli .
In figura è rappresentata la circonferenza goniometrica. Il raggio della circonferenza goniometrica vale 1. Sia P un punto vincolato a percorrere la circonferenza in senso antiorario. Le coordinate del punto P sono rispettivamente cosx e sinx. L'ordinata del punto T è la tanx e l'ascissa del punto C è la cotx. Per semplificare le notazioni, l'angolo "variabile" POK è stato indicato come angolo x come già è stato spiegato in funzioni goniometriche.
Per definizione si ha quindi che:
OP=1
PH=sinx
OH=cosx
AT=tanx
EC=cotx
Considerato che il triangolo OPH è rettangolo, per il teorema di Pitagora si avrà HP2+OH2=1 ovvero sostituendo si ricava quella che viene chiamata la prima relazione fondamentale della trigonometria:

Si considerino i due triangoli OTA e OPH, essi sono simili poiché sono entrambi triangoli rettangoli ed hanno un angolo in comune. Dalla similitudine ne consegue la seguente proporzione: PH:OH= TA:OK ovvero sinx:cosx=tanx:1 da ciò si ricava quella che viene chiamata la seconda relazione fondamentale della trigonometria:

Si considerino i due triangoli OTA e OPH, essi sono simili poiché sono entrambi triangoli rettangoli ed hanno l'angolo POH uguale a EOC. I due triangoli sono simili da cui ne consegue la seguente proporzione: EC:OE=OH:PH ovvero =cotx:1=cosx:sinx da ciò si ricava: cotx=cosx/sinx, ovvero la cotangente è la funzione reciproca della tangente.
A destra in figura, supponiamo di avere un triangolo rettangolo con angolo retto in A e con l'angolo γ uguale all'angolo x della circonferenza goniometrica. I due triangoli ABC e POH sono simili, poiché hanno due angoli uguali.
I lati dei due triangoli sono quindi proporzionali e si possono scrivere le seguenti proporzioni:
OP:PH=CB:AB ovvero, tenendo presente che il raggio della circonferenza trigonometrica è 1 1:sinx=a:c da cui sinx=c/a da cui c=a*sinx, generalizzando, un cateto è dato dal prodotto dell'ipotenusa moltiplicata per il seno dell'angolo opposto.


OP:OH=a:b ovvero 1:cosx=a:b da cui cosx=b/a da cui b=a*cosx, generalizzando, un cateto è dato dal prodotto dell'ipotenusa moltiplicata per il coseno dell'angolo adiacente.
PH:OH=AB:AC ovvero sinx:cosx=c:b da cui sinx/cosx=c/b ovvero dato che tanx=sinx/cosx, tanx=c/b da cui c=btanx, generalizzando, un cateto è dato dal prodotto dell'altro cateto moltiplicato per la tangente dell'angolo opposto.
Si sono individuate quindi, le seguenti relazioni:
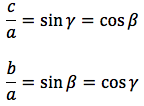
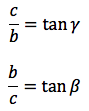
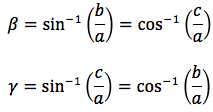
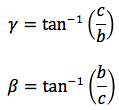
Vedremo la dimostrazione di alcuni teoremi che serviranno a rendere più semplici le dimostrazioni del teorema dei seni ed il teorema del coseno.
Teorema: L'angolo al centro della circonferenza è il doppio di un qualsiasi angolo alla circonferenza che insiste sullo stesso arco.
Dimostrazione
Dividiamo la dimostrazione del teorema in tre casi.
Il primo caso è caratterizzato dal fatto che il lato dell'angolo alla circonferenza CA passa per il centro della circonferenza O. Va dimostrato che l'angolo alla circonferenza ACB che in figura è indicato con α è la metà dell'angolo al cento AOB, entrambi gli angoli insistono infatti sullo stesso arco AB. Si consideri il triangolo BOC. Si tratta di un triangolo isoscele in quanto due lati BO e OC corrispondono al raggio della circonferenza. Gli angoli opposti ai due lati uguali sono pure essi uguali.
In figura sono indicati con α. L'angolo BOC è 180o-2α in quanto la somma degli angoli interni di un qualsiasi triangolo è 180o. L'angolo BOC sommato all'angolo AOB deve dare 180o, l'angolo AOB dev'essere quindi 2α che è quello che si voleva dimostrare.
Il secondo caso prevede che il centro della circonferenza O è contenuto nell'angolo alla circonferenza DCB.
In figura è disegnato il diametro COA per meglio notare che l'angolo AOB è il doppio dell'angolo ACB infatti siamo ricaduti nel caso 1, analogamente l'angolo AOD è il doppio dell'angolo ACD. L'angolo DOB può essere espresso come somma degli angoli DOA e AOB ovvero DOB=2α+2β=2(α+β) e analogamente l'angolo BCD può essere espresso come somma degli angoli BCA e ACD ovvero BCD=α+β.
Dalle due relazioni: DOB=2(α+β) e BCD= α+β, si può quindi concludere che l'angolo DOB è il doppio dell'angolo BCD.
Nel terzo caso il centro della circonferenza O è esterno all'angolo alla circonferenza DCB.
In figura è disegnato il diametro COA per meglio notare che l'angolo AOB è il doppio dell'angolo ACB infatti siamo ricaduti nel caso 1, analogamente l'angolo AOD è il doppio dell'angolo ACD.
L'angolo DOB può essere espresso come differenza degli angoli AOB E AOD ovvero DOB=2α-2β=2(α-β) e analogamente l'angolo BCD può essere espresso come differenza degli angoli ACB e ACD ovvero BCD=α-β.
Dalle due relazioni: DOB=2(α-β) e BCD= α+β, si può quindi concludere che l'angolo DOB è il doppio dell'angolo BCD.
In questo modo, suddividendo la dimostrazione nei tre casi visti, si sono considerati tutti i casi possibili.



Teorema: Un triangolo inscritto in una semicirconferenza è rettangolo.
Dimostrazione
Nella figura è rappresentato un triangolo inscritto in una semicirconferenza ovvero l'ipotenusa del triangolo corrisponde al diametro della circonferenza.
L'angolo in B è un angolo alla circonferenza che insiste su di un arco uguale alla semicirconferenza. L'angolo in O è invece un angolo al centro della circonferenza che insiste sullo stesso arco.
L'angolo in O è un angolo piatto quindi per il teorema precedente, ovvero per il teorema dell'angolo al centro, l'angolo in B è la sua metà ovvero un angolo retto.

Teorema: Un quadrilatero inscritto in una circonferenza ha gli angoli opposti supplementari.
Dimostrazione
Nella figura è rappresentato un quadrilatero ABCD inscritto in una circonferenza.
L'angolo β che ha il vertice in C, per il teorema visto in precedenza, è la metà dell'angolo al centro della circonferenza che insiste sull'arco DAB, che in figura è l'arco piu' piccolo. Analogamente l'angolo α che ha vertice in A è la metà dell'angolo al centro della circonferenza che insiste sull'arco DCB ovvero, in figura, quello che è l'arco più grande. La somma di 2α+2β costituisce un angolo giro, per cui α+β è la meta' ovvero un angolo piatto, quindi α e β sono due angoli supplementari, ma α e β sono proprio i due angoli opposti del quadrilatero inscritto.

Teorema: In una circonferenza, la misura di una corda, è data dal prodotto del diametro moltiplicato per il seno per l'angolo alla circonferenza (indifferentemente uno dei due angoli alla circonferenza) che insiste sulla corda.
Dimostrazione
Nella figura è rappresentato un angolo alla circonferenza che insiste sull'arco AB, quello minore.
L'angolo che ha vertice in D è uguale all'angolo alla circonferenza che ha un lato corrispondente al diametro in figura l'angolo in C.
Questi due angoli sono uguali tra loro in quanto entrambi insistono sull'arco AB e quindi entrambi sono la metà dell'angolo al centro che insiste sullo stesso arco.
In figura vengono infatti indicati entrambi con α.
Il triangolo ABC avendo l'ipotenusa corrispondente al diametro è un triangolo rettangolo, possiamo scrivere quindi le relazioni individuate per i triangoli rettangoli ovvero
AB=AC sinα
ovvero
AB=2r sinα
dove si è indicato con r il raggio della circonferenza, che è cio che si vuol dimostrare.
Nella figura di sotto si è considerato l'angolo alla circonferenza che insiste sull'arco AB maggiore.
In tal caso l'angolo ADB è 180o-α e questo lo si ottiene applicando, al quadrilatero ADBC, il teorema del quadrilatero inscritto in una circonferenza.
Dalla relazione sin180o-α=sinα si può quindi affermare che il teorema della corda rimane valido anche in tal caso.


Teorema: In un triangolo è costante il rapporto tra la misura di ciascun lato e il seno dell'angolo opposto.
Dimostrazione
Si noti che un triangolo è sempre inscrittibile in una circonferenza. In figura al triangolo ABC possiamo applicare il teorema della corda da cui:
a=2rsinα b=2rsinβ c=2rsinγ
dove r è il raggio della circonferenza che inscrive il triangolo.
Da tali relazioni ne consegue che:
2r=a/sinα 2r=b/sinβ 2r=c/sinγ
e per la proprietà transitiva dell'uguaglianza:
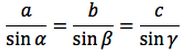

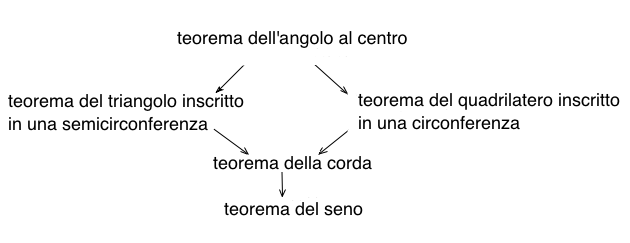
Per memorizzare meglio la sucessione dei teoremi che portano alla dimostrazione del teorema dei seni, si noti che dal teorema dell'angolo al centro ne conseguono i teoremi del triangolo inscritto in una semicirconferenza e del quadrilatero inscritto in una circonferenza. Da questi due teoremi ne consegue il teorema della corda dal quale poi a sua volta ne deriva il teorema dei seni. Questi cinque teoremi sono dunque legati al seguente schema.
Leonhard Euler, (Basilea, 15 aprile 1707 - San Pietroburgo, 18 settembre 1783), matematico e fisico. E' noto per aver fornito contributi importanti in diversi campi della matematica e della fisica. Il suo nome viene associato a diverse formule, teoremi, metodi, criteri, relazioni, equazioni. In geometria: il cerchio, la retta e i punti di Eulero relativi ai triangoli, la relazione di Eulero, che riguardava il cerchio circoscritto a un triangolo; il criterio di Eulero nella teoria dei numeri, l'indicatore di Eulero, l'identita' di Eulero. In fisica: il carico critico di Eulero, il diagramma di Eulero-Venn; per rappresentare gli insiemi la relazione di Eulero nella teoria dei grafi; il metodo di Eulero (relativo alla soluzione delle equazioni di quarto grado); il metodo di Eulero riguardante le equazioni differenziali. Buona parte della simbologia matematica tuttora in uso si deve a Eulero, per esempio i per i numeri immaginari, ∑ come simbolo per la sommatoria, f(x) per indicare una funzione. Diffuse l'uso della lettera π per indicare pi greco.
Teorema: In un triangolo un lato è dato dalla somma degli altri due lati moltiplicati ciascuno per il coseno dell'angolo adiacente al lato stesso.
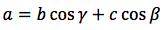
Dimostrazione
In figura H sia il piede dell'altezza relativa al lato a, i due triangoli ABH ed ACH sono rettangoli in quanto l'angolo in H è retto, si può quindi scrivere che BC=BH+HC, applichiamo quindi le relazioni relative ai triangoli rettangoli per cui:
CH=b cosγ, HB=c cosβ per cui:
a=b cosγ+c cosβ
La relazione rimane valida anche nel caso in cui β sia un angolo ottuso, anche in questo caso H sia il piede dell'altezza relativa al lato a, i due triangoli ABH ed ACH sono rettangoli in quanto l'angolo in H è retto, quindi:
CB=CH-BH
ma CH=b cos γ e BH=c cos(180o-β) quindi:
a=b cosγ-c cos(180o-β) ma cos(180o-β)=-cosβ, per cui
a=b cosγ-(-c cos(β) ovvero:
a=b cosγ+c cosβ


Teorema: in un triangolo un lato al quadrato è dato dalla somma degli altri due lati al quadrato da cui si deve togliere il prodotto degli altri due lati moltiplicati per il coseno dell'angolo che sta opposto al lato stesso.
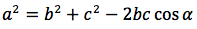
Dimostrazione
Per il teorema delle proiezioni si può scrivere:
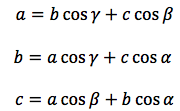
moltiplicando per a la prima relazione, per -b la seconda e per -c la terza si ottiene:
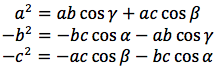
sommando membro a membro i termini delle tre relazini e semplificando:
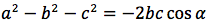
ricaviamo a:
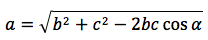
Se l'angolo compreso è retto il coseno dell'angolo retto è zero per cui il teorema del coseno si trasforma nel teorema di Pitagora, per questo motivo il teorema del coseno oltre che teorema di Carnot, viene anche chiamato teorema di Pitagora generalizzato.
Con opportuni semplici accorgimenti si ricavano analoghe formule oltre che per il lato a pure per i lati b, c:
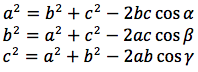
Si può ricavare anche il cosα in funzione dei lati:
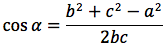
e con la funzione inversa, arcocoseno, si determina l'angolo α in funzione dei tre lati:
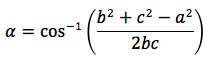
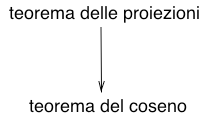
Si noti che dal teorema delle proiezioni ne consegue il teorema del coseno, questi due teoremi sono dunque legati al seguente schema.
Lazare Nicolas Marguerite Carnot (1753-1823) fu generale, matematico, fisico e politico francese. Membro della Convenzione Nazionale e del Direttorio durante la rivoluzione francese.
In un triangolo ci sono tre lati e tre angoli, risolvere un triangolo significa dati tre elementi, che non siano contemporaneamente tre angoli, trovare gli altri tre. Il problema in cui siano noti i tre angoli è un problema indeterminato ci sono infatti infiniti triangoli, tutti simili, che hanno tre angoli uguali.
In un triangolo rettangolo un elemento è noto ed è l'angolo retto, risolvere un triangolo rettangolo significa quindi, dati due elementi, che non siano contemporaneamente due angoli, trovare gli altri tre elementi. Quindi oltre all'angolo retto vengono dati altri due elementi.
In quanti modi possiamo scegliere due elementi in un insieme di 5 elementi?
La tabella rappresenta tutti i possibili problemi che possono essere proposti per la risoluzione di triangoli rettangoli. Si sa che il triangolo ha un angolo retto α=90° oltre a questa informazione, i dati di partenza del problema sono due e possono essere scelti in un insieme di cinque elementi. Ci si chiede quindi in un insieme di cinque elementi, quanti sono i suoi sottoinsiemi di due elementi.
La risposta è 10 ovvero le combinazioni (5,2). Uno dei 10 possibili problemi risulta essere indeterminato, p il caso in cui sono dati i due angoli per cui in totale si possono considerare 9 casi. In effetti però si puo pensare che alcuni problemi sono del tutto analoghi tanto da poter pensare di ridurre il tutto a quattro problemi:
| β | γ | a | b | c | dati |
| X | X | 2 angoli | |||
| X | X | ipotenusa e angolo adiacente | |||
| X | X | ipotenusa e angolo adiacente | |||
| X | X | cateto e angolo adiacente | |||
| X | X | cateto e angolo adiacente | |||
| X | X | cateto e angolo opposto | |||
| X | X | cateto e angolo opposto | |||
| X | X | ipotenusa e cateto | |||
| X | X | ipotenusa e cateto | |||
| X | X | due cateti |
Sono dati ipotenusa e angolo adiacente (2 casi)
Si determina la misura del cateto opposto all'angolo dato, moltiplicando l'ipotenusa per il seno dell'angolo. Per determinare il cateto adiacente si moltiplica l'ipotenusa per il coseno dell'angolo dato. Per determinare infine la misura dell'angolo si usano le funzioni inverse.
Sono dati cateto e angolo adiacente (2 casi)
Si determina la misura dell'altro cateto moltiplicando il cateto per la tangente dell'angolo. L'ipotenusa può determinarsi con il teorema di Pitagora oppure moltiplicando la misura, del cateto trovato, per la tangente dell'angolo dato. Il terzo angolo si determina per differenza, sapendo che la somma degli angoli interni di un triangolo è 180o.
Sono dati cateto e angolo opposto (2 casi)
Si determina l'ipotenusa dividendo il cateto per il seno dell'angolo. L'alto cateto si può determinare o con il teorema di Pitagora oppure dividendo il cateto dato per la tangente dell'angolo dato. Il terzo angolo si determina per differenza, sapendo che la somma degli angoli interni di un triangolo è 180°.
Sono dati due lati, ovvero 2 cateti (1 caso), oppure ipotenusa e angolo adiacente (2 casi)
Si usa il teorema di Pitagora per calcolare il terzo lato, quindi attraverso l'uso delle funzioni inverse si determinano gli angoli.
Riassumendo le relazioni alle quali si deve far riferimento, per la risoluzione dei triangoli rettangoli, sono le seguenti:
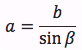 | 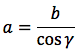 | 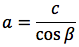 | 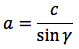 |
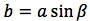 | 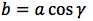 | 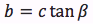 | 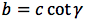 |
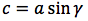 | 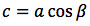 | 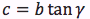 | 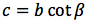 |
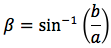 | 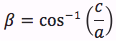 | 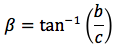 | 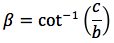 |
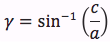 | 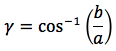 | 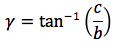 | 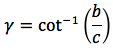 |
Nelle ultime due colonne sono ricavati gli angoli in funzione dei lati adoperando per lo scopo, le funzioni goniometriche inverse. Le notazioni che qui sono state usate per tali funzioni arcoseno, arcocoseno arcotangente sono quelle della calcolatrice portatile ovvero sin-1, cos-1, tan-1.
Per approfondire le procedure di risoluzione dei triangoli si rimanda comunque alla parte esercitazioni.
Gli strumenti utili per la risoluzione dei triangoli qualunque sono dunque, il teorema del seno ed il teorema del coseno.
Si tenga presente che, potrebbe non esistere un triangolo con i dati assegnati per cui un problema potrebbe anche essere impossibile, per esempio se vengono dati tre lati, dove la somma di due risulti essere minore del terzo lato. Un problema potrebbe avere anche due soluzioni, ovvero potrebbero esistere due triangoli con i dati assegnati, è il caso in cui sono dati due lati ed un angolo non compreso.
La funzione arcoseno può determinare angoli fino a 90°, però la soluzione potrebbe anche essere un triagolo ottusangolo quindi oltre all'eventuale angolo α va preso in considerazione anche l'angolo 180°-α in quanto sinα=sin(180-α).
Perchè una soluzione sia accettabile è necessario che ad angolo maggiore sia opposto lato maggiore e che ad che ad angolo minore sia opposto lato minore.
A volte un'angolo può essere trovato in due modi diversi per esempio con la funzione arcoseno, attraverso il teorema del seno, oppure con una differenza tenendo conto che la somma degli angoli interni del triangolo è 180° si consiglia di calcolare la misura dell'angolo in entrambe le maniere per verificarne l'esatezza del risultato.
E' necessario dotarsi di una calcolatrice scientifica per il calcolo dei valori delle funzioni goniometrice sin, cos, tan, e delle relative inverse sin-1 cos-1 tan-1.
La tabella di sinistra, rappresenta tutti i possibili problemi che possono essere proposti per la risoluzione di triangoli. I dati del problema sono tre e possono essere scelti in un insieme di sei elementi. Ci si chiede quindi in un insieme di sei elementi, quanti sono i suoi sottoinsiemi di tre elementi. La risposta è 20 ovvero le combinazioni (6,3). Uno dei 20 possibili problemi risulta essere indeterminato ed è il caso in cui sono dati i tre angoli. Rimangono 19 problemi da poter assegnare, ma alcuni di questi sono del tutto analoghi tanto da poter pensare di ridurre il tutto a quattro soli problemi ovvero:
| α | β | γ | a | b | c | dati |
| X | X | X | 3 lati | |||
| X | X | X | 2 lati e 1 angolo non compreso | |||
| X | X | X | 2 lati e 1 angolo non compreso | |||
| X | X | X | 2 lati e 1 angolo non compreso | |||
| X | X | X | 2 lati e 1 angolo non compreso | |||
| X | X | X | 2 lati e 1 angolo non compreso | |||
| X | X | X | 2 lati e 1 angolo non compreso | |||
| X | X | X | 2 lati e angolo compreso | |||
| X | X | X | 2 lati e angolo compreso | |||
| X | X | X | 2 lati e angolo compreso | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 1 lato e 2 angoli | |||
| X | X | X | 3 angoli |
Sono dati 3 lati (1 caso)
Se la somma di due lati è minore dell'altro lato il problema è impossibile altrimenti c'è un'unica soluzione. Si usa teorema del coseno e attraverso la funzione inversa, arcocoseno, si individuano i tre angoli.
Sono dati 2 lati e 1 angolo non compreso (6 casi)
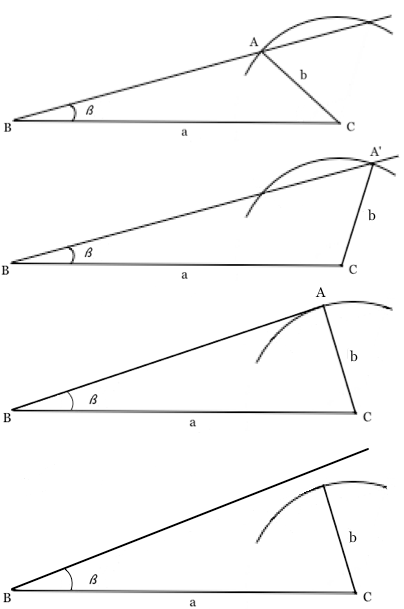
Per comprendere meglio le varie situazioni che possono capitare, mettiamoci nei panni di un disegnatore dotato di compasso, righelli, goniometro che, avendo a disposizione i dati del problema ovvero a, b e β, debba disegnare il triangolo. Per prima cosa aiutandosi con il righello, disegna il lato a, quindi con il goniometro prende la misura di β e disegna la semiretta su cui si andrà a costruire il lato c. A questo punto prende il compasso e misura un'apertura pari al lato b, puntando su C disegna un arco di circonferenza.
Si possono verificare tre ipotesi. Le prime due figure riguardano la prima di queste ipotesi, ovvero la semiretta intercetta l'arco di circonferenza, di origine B, in due punti; ciò significa che ci sono due soluzioni ovvero si possono costruire due triangoli con i due lati a, b e l'angolo β uguali. Nelle prime due figure i due triangoli vengono indicati rispettivamente con ABC e ABC'.
Nella terza figura è illustrato il caso che la semiretta intercetti l'arco di circonferenza in un solo punto, la semiretta risulta tangente all'arco di circonferenza, la soluzione è quindi unica e l'angolo in A è retto.
Nella quarta figura, potrebbe capitare che la semiretta non intercetti l'arco di circonferenza in alcun punto, in tale ipotesi non ci sono soluzioni, ovvero il problema è impossibile.
Potrebbe anche verificarsi il caso, illustrato nella quinta figura, che la semiretta intercetti l'arco di circonferenza in un solo punto senza che la semiretta stessa risulti essere tangente all'arco di circonferenza e anche in tal caso la soluzione sarà unica.
Per risolvere tale problema, si parte con il teorema del seno e si ricava α con la funzione sin-1. E' necessario tener presente che, oltre all'angolo α, individuato dalla calcolatrice, potrebbe essere accettabile anche l'angolo 180-α, va verificato sempre, che ad angolo maggiore sia opposto il lato maggiore affinchè la soluzione sia accettabile.
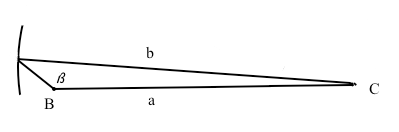
Sono dati 2 lati e angolo compreso (3 casi)
Con questi dati ci sarà sempre e comunque una soluzione unica. Si usa il teorema del coseno per trovare il terzo lato. Per trovare gli angoli poi si usa o il teorema dei seni o il teorema del coseno.
Sono dati 1 lato e 2 angoli (9 casi)
Se la somma degli angoli dati fosse maggiore o uguale a 90° ovviamente il problema sarebbe impossibile. Escludendo tale ipotesi la soluzione sarà unica. Si determina la misura dell'altro angolo tenendo conto che la somma degli angoli interni è 180° quindi si usa teorema dei seni per calcolare i lati.
Riassumendo le relazioni alle quali si deve far riferimento, per la risoluzione dei triangoli, sono le seguenti:
| Teorema dei seni | Teorema del coseno | ||
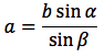 | 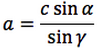 | 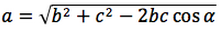 | |
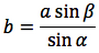 | 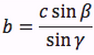 | 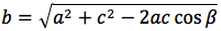 | |
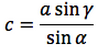 | 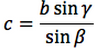 | 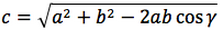 | |
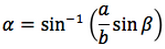 | 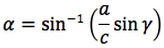 | 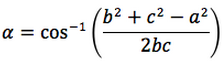 | |
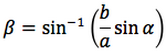 | 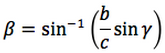 | 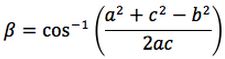 | |
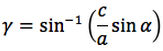 | 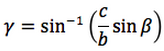 | 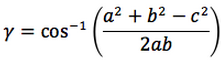 | |
Nelle prime due colonne si trovano le formule dedotte dal teorema dei seni, nella terza colonna si trovano le formule dedotte dal teorema del coseno. Nelle ultime tre righe sono ricavati gli angoli in funzione dei lati adoperando per lo scopo, le funzioni goniometriche inverse.
Le notazioni che qui sono state usate per tali funzioni arcoseno, arcocoseno, arcotangente, sono quelle della calcolatrice scientifica ovvero: sin-1, cos-1, tan-1.
Per approfondire le procedure di risoluzione dei triangoli si rimanda comunque alla parte esercitazioni.