Risoluzione triangoli
In un triangolo ci sono tre lati e tre angoli, risolvere un triangolo significa dati tre elementi, che non siano contemporaneamente tre angoli, trovare gli altri tre. Il problema in cui siano noti i tre angoli è un problema indeterminato ci sono infatti infiniti triangoli, tutti simili, che hanno tre angoli uguali.
Risoluzione triangoli rettangoli
In un triangolo rettangolo un elemento è noto ed è l'angolo retto, risolvere un triangolo rettangolo significa quindi, dati due elementi, che non siano contemporaneamente due angoli, trovare gli altri due elementi.
Quindi oltre all'angolo retto vengono dati altri due elementi.
In quanti modi possiamo scegliere due elementi in un insieme di 5 elementi?
La tabella rappresenta tutti i possibili problemi che possono essere proposti per la risoluzione di triangoli rettangoli. Si sa che il triangolo ha un angolo retto α=90° oltre a questa informazione, i dati di partenza del problema sono due e possono essere scelti in un insieme di cinque elementi.
Ci si chiede quindi in un insieme di cinque elementi, quanti sono i suoi sottoinsiemi di due elementi. La risposta è 10 ovvero le combinazioni (5,2). Uno dei 10 possibili problemi risulta essere indeterminato, si tratta del primo caso in cui sono dati i due angoli. In totale si possono considerare quindi, 9 casi.
Si puo pensare però, che alcuni problemi sono analoghi, tanto da poter ridurre il tutto all'analisi di quattro casi:
| casi | β | γ | a | b | c | dati |
| 1 | X | X | 2 angoli | |||
| 2 | X | X | ipotenusa e angolo adiacente | |||
| 3 | X | X | ipotenusa e angolo adiacente | |||
| 4 | X | X | cateto e angolo adiacente | |||
| 5 | X | X | cateto e angolo adiacente | |||
| 6 | X | X | cateto e angolo opposto | |||
| 7 | X | X | cateto e angolo opposto | |||
| 8 | X | X | ipotenusa e cateto | |||
| 9 | X | X | ipotenusa e cateto | |||
| 10 | X | X | due cateti |
Sono dati ipotenusa e angolo adiacente (casi 2,3)
Si determina la misura del cateto opposto all'angolo dato, moltiplicando l'ipotenusa per il seno dell'angolo. Per determinare il cateto adiacente si moltiplica l'ipotenusa per il coseno dell'angolo dato. Per determinare infine la misura dell'angolo si usano le funzioni inverse.
Sono dati cateto e angolo adiacente (casi 4,5)
Si determina la misura dell'altro cateto moltiplicando il cateto per la tangente dell'angolo. L'ipotenusa può determinarsi con il teorema di Pitagora oppure moltiplicando la misura, del cateto trovato, per la tangente dell'angolo dato. Il terzo angolo si determina per differenza, sapendo che la somma degli angoli interni di un triangolo è 180o.
Sono dati cateto e angolo opposto (casi 6,7)
Si determina l'ipotenusa dividendo il cateto per il seno dell'angolo. L'alto cateto si può determinare o con il teorema di Pitagora oppure dividendo il cateto dato per la tangente dell'angolo dato. Il terzo angolo si determina per differenza, sapendo che la somma degli angoli interni di un triangolo è 180°.
Sono dati due lati, ovvero 2 cateti (caso 10), oppure ipotenusa e cateto (casi 8,9)
Si usa il teorema di Pitagora per calcolare il terzo lato, quindi attraverso l'uso delle funzioni inverse si determinano gli angoli.
Riassumendo le relazioni alle quali si deve far riferimento, per la risoluzione dei triangoli rettangoli, sono le seguenti:
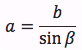 | 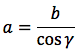 | 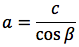 | 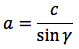 |
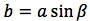 | 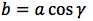 | 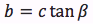 | 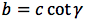 |
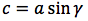 | 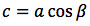 | 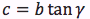 | 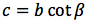 |
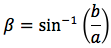 | 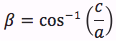 | 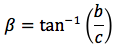 | 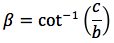 |
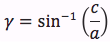 | 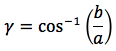 | 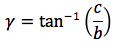 | 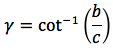 |
Nelle ultime due colonne sono ricavati gli angoli in funzione dei lati adoperando per lo scopo, le funzioni goniometriche inverse. Le notazioni che qui sono state usate per tali funzioni arcoseno, arcocoseno arcotangente sono quelle della calcolatrice portatile ovvero sin-1, cos-1, tan-1.
Per approfondire le procedure di risoluzione dei triangoli si rimanda comunque alla parte esercitazioni.
Risoluzione triangoli qualunque
Gli strumenti utili per la risoluzione dei triangoli qualunque sono dunque, il teorema del seno ed il teorema del coseno.
Si tenga presente che, potrebbe non esistere un triangolo con i dati assegnati per cui un problema potrebbe anche essere impossibile, per esempio se vengono dati tre lati, dove la somma di due risulti essere minore del terzo lato. Un problema potrebbe avere anche due soluzioni, ovvero potrebbero esistere due triangoli con i dati assegnati, è il caso in cui sono dati due lati ed un angolo non compreso.
La funzione arcoseno può determinare angoli fino a 90°, però la soluzione potrebbe anche essere un triagolo ottusangolo quindi oltre all'eventuale angolo α va preso in considerazione anche l'angolo 180°-α in quanto sinα=sin(180-α).
Perchè una soluzione sia accettabile è necessario che ad angolo maggiore sia opposto lato maggiore e che ad che ad angolo minore sia opposto lato minore.
A volte un'angolo può essere trovato in due modi diversi per esempio con la funzione arcoseno, attraverso il teorema del seno, oppure con una semplice differenza tenendo conto che la somma degli angoli interni del triangolo è 180°. E' consigliabile calcolare la misura dell'angolo in entrambe le maniere per verificarne l'esatezza del risultato.
E' necessario dotarsi di una calcolatrice scientifica per il calcolo dei valori delle funzioni goniometrice sin, cos, tan, e delle relative inverse sin-1 cos-1 tan-1. La tabella a lato, riporta tutti i possibili problemi che possono essere proposti per la risoluzione di triangoli. Nel caso in cui i dati del problemo sono i tre angoli ovviamente il problema risulta indeterminato, infatti esistono infiniti triangoli con tre angoli uguali.
I dati del problema sono tre e possono essere scelti in un insieme di sei elementi pertanto in totale si contano 20 casi.
Ci si chiede quindi in un insieme di sei elementi, quanti sono i suoi sottoinsiemi di tre elementi. La risposta è 20 ovvero le combinazioni (6,3). Uno dei 20 possibili problemi risulta essere indeterminato ed è il caso in cui sono dati i tre angoli. Rimangono 19 problemi da poter assegnare, ma alcuni di questi sono del tutto analoghi tanto da poter pensare di ridurre il tutto a quattro soli problemi ovvero:| casi | α | β | γ | a | b | c | dati |
| 1 | X | X | X | 3 lati | |||
| 2 | X | X | X | 2 lati e 1 angolo non compreso | |||
| 3 | X | X | X | 2 lati e 1 angolo non compreso | |||
| 4 | X | X | X | 2 lati e 1 angolo non compreso | |||
| 5 | X | X | X | 2 lati e 1 angolo non compreso | |||
| 6 | X | X | X | 2 lati e 1 angolo non compreso | |||
| 7 | X | X | X | 2 lati e 1 angolo non compreso | |||
| 8 | X | X | X | 2 lati e angolo compreso | |||
| 9 | X | X | X | 2 lati e angolo compreso | |||
| 10 | X | X | X | 2 lati e angolo compreso | |||
| 11 | X | X | X | 1 lato e 2 angoli | |||
| 12 | X | X | X | 1 lato e 2 angoli | |||
| 13 | X | X | X | 1 lato e 2 angoli | |||
| 14 | X | X | X | 1 lato e 2 angoli | |||
| 15 | X | X | X | 1 lato e 2 angoli | |||
| 16 | X | X | X | 1 lato e 2 angoli | |||
| 17 | X | X | X | 1 lato e 2 angoli | |||
| 17 | X | X | X | 1 lato e 2 angoli | |||
| 18 | X | X | X | 1 lato e 2 angoli | |||
| 20 | X | X | X | 3 angoli |
Sono dati 3 lati (caso 1):
Se la somma di due lati è minore dell'altro lato il problema è impossibile altrimenti c'è un'unica soluzione. Si usa teorema del coseno e attraverso la funzione inversa, arcocoseno, si individuano i tre angoli.
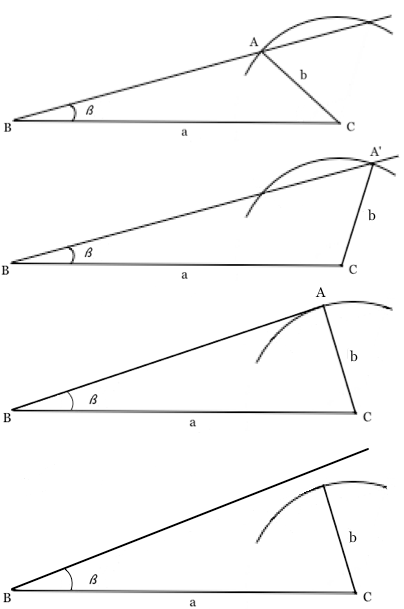
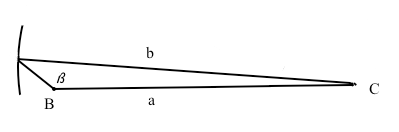
Sono dati 2 lati e 1 angolo non compreso (casi 2,3,4,5,6,7):
Per comprendere meglio le varie situazioni che possono capitare, mettiamoci nei panni di un disegnatore dotato di compasso, righelli, goniometro che, avendo a disposizione i dati del problema ovvero a, b e β, debba disegnare il triangolo. Per prima cosa aiutandosi con il righello, disegna il lato a, quindi con il goniometro prende la misura di β e disegna la semiretta su cui si andrà a costruire il lato c. A questo punto prende il compasso e misura un'apertura pari al lato b, puntando su C disegna un arco di circonferenza. Si possono verificare tre ipotesi. Le prime due figure riguardano la prima di queste ipotesi, ovvero la semiretta intercetta l'arco di circonferenza, di origine B, in due punti; ciò significa che ci sono due soluzioni ovvero si possono costruire due triangoli con i due lati a, b e l'angolo β uguali. Nelle prime due figure i due triangoli vengono indicati rispettivamente con ABC e ABC'. Nella terza figura è illustrato il caso che la semiretta intercetti l'arco di circonferenza in un solo punto, la semiretta risulta tangente all'arco di circonferenza, la soluzione è quindi unica e l'angolo in A è retto. Nella quarta figura, potrebbe capitare che la semiretta non intercetti l'arco di circonferenza in alcun punto, in tale ipotesi non ci sono soluzioni, ovvero il problema è impossibile. Potrebbe anche verificarsi il caso, illustrato nella quinta figura, che la semiretta intercetti l'arco di circonferenza in un solo punto senza che la semiretta stessa risulti essere tangente all'arco di circonferenza e anche in tal caso la soluzione sarà unica. Per risolvere tale problema, si parte con il teorema del seno e si ricava α con la funzione sin-1. E' necessario tener presente che, oltre all'angolo α, individuato dalla calcolatrice, potrebbe essere accettabile anche l'angolo 180-α, va verificato sempre, che ad angolo maggiore sia opposto il lato maggiore affinchè la soluzione sia accettabile.
Sono dati 2 lati e angolo compreso (casi 8,9,10):
Con questi dati ci sarà sempre e comunque una soluzione unica. Si usa il teorema del coseno per trovare il terzo lato. Per trovare gli angoli poi si usa o il teorema dei seni o il teorema del coseno.
Sono dati 1 lato e 2 angoli (casi 11,12,13,14,15,16,17,18):
Se la somma degli angoli dati fosse maggiore o uguale a 90° ovviamente il problema sarebbe impossibile. Escludendo tale ipotesi la soluzione sarà unica. Si determina la misura dell'altro angolo tenendo conto che la somma degli angoli interni è 180° quindi si usa teorema dei seni per calcolare i lati.
Riassumendo le relazioni alle quali si deve far riferimento, per la risoluzione dei triangoli, sono le seguenti:
| Teorema dei seni | Teorema del coseno | ||
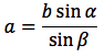 | 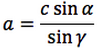 | 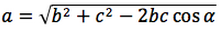 | |
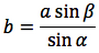 | 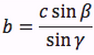 | 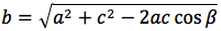 | |
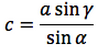 | 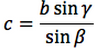 | 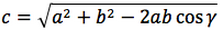 | |
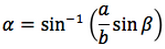 | 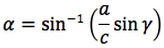 | 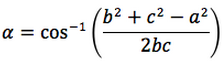 | |
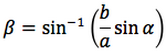 | 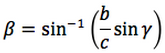 | 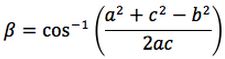 | |
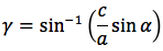 | 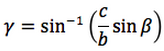 | 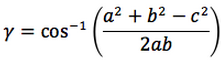 | |
Nelle prime due colonne si trovano le formule dedotte dal teorema dei seni, nella terza colonna si trovano le formule dedotte dal teorema del coseno. Nelle ultime tre righe sono ricavati gli angoli in funzione dei lati adoperando per lo scopo, le funzioni goniometriche inverse.
Le notazioni che sono state usate per le funzioni arcoseno, arcocoseno, arcotangente, sono quelle della calcolatrice scientifica ovvero: sin-1, cos-1, tan-1.
Per approfondire le procedure di risoluzione dei triangoli si rimanda comunque alla parte esercitazioni.